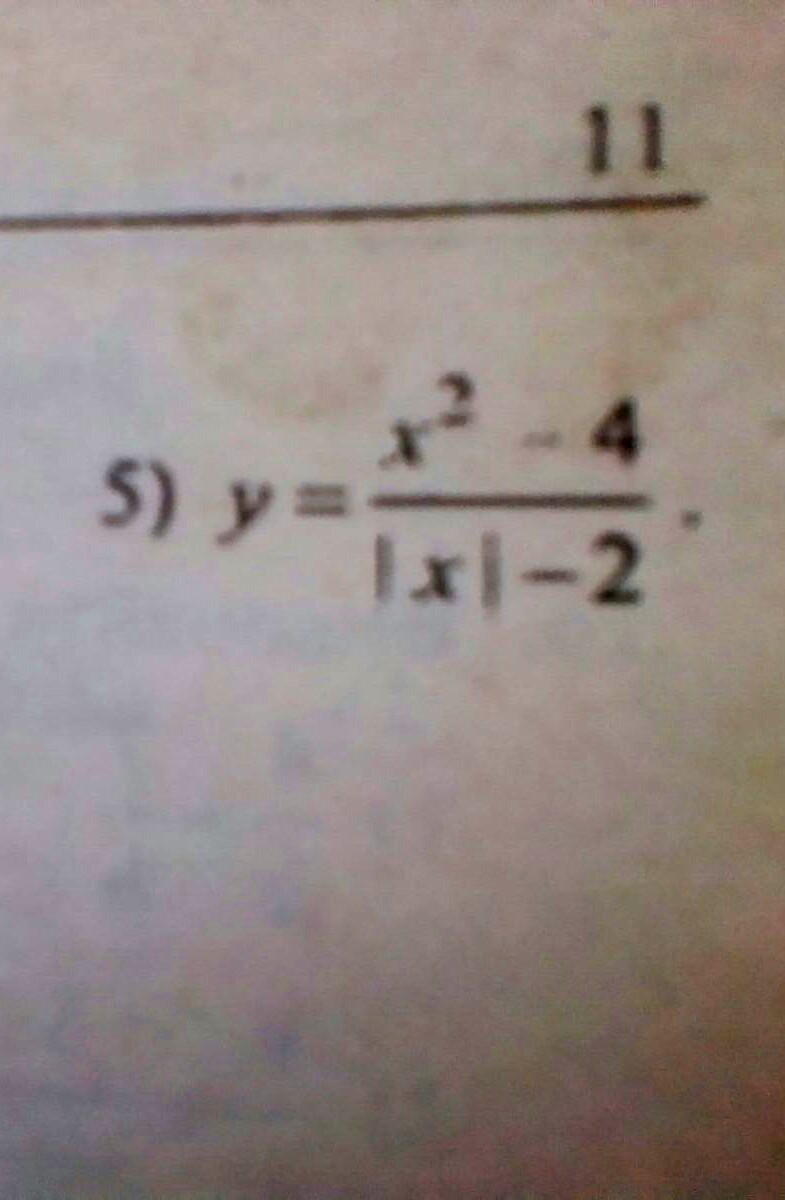Ответы 1
-
найдем точки, в которых эта функция не существует:
теперь раскрываем модуль и получаем 2 функции:
строим графики:1) линейная функция => для построения графика нужны 2 точкиx=0; y=2 (0;2)x=1; y=3 (1;3)x=2; y=4 (2;4) - выколотая точкастроим график на промежутке [0;+oo)2) тоже линейная фукнцияx=0; y=2 (0;2)x=-1; y=3 (-1;3)x=-2; y=4 (-2;4) - выколотая точкастроим график на промежутке (-oo;0]график в приложении( точки (-2;4) и (2;4) - выколотые)

-
Автор:
watkins - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Какой фразеологизм означает много.Куры не клюют,или делать из мухи слона
-
Предмет:
Русский язык -
Автор:
frankycross - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
помогите пожалуйста ! Как будет на английском " Около моей школы растут цветы"
-
Предмет:
Английский язык -
Автор:
cordova - 5 лет назад
-
Ответов:
3 -
Смотреть
-
-
Определите тип и стиль текста.
Много хорошеньких вещиц из кости и из дерева на письменном столе; почему-то преобладают фигуры слонов. На стенах портреты Толстого, Григоровича, Тургенева. На отдельном маленьком столике, на веерообразной подставке, множество фотографий артистов и. писателей.
По обоим бокам окна спускаются прямые, тяжелые темные занавески, на полу большой ковер с восточным рисунком. Эта драпировка смягчает все контуры и еще больше темнит кабинет, но благодаря ей ровнее и приятнее ложится свет из окна на письменный стол. Пахнет тонкими духами, до которых Антон Павлович всегда был охотник. Из окна видна открытая подковообразная лощина, спускающаяся далеко к морю, и самое море, окруженное амфитеатром домов.-
Предмет:
Русский язык -
Автор:
taco - 5 лет назад
-
Ответов:
2 -
Смотреть
-
- . Почему лимфатические узлы нельзя массировать? 3. Каково значение венозных каналов?
How much to ban the user?
1 hour
1 day
100 years