45 баллов :)Ответ фотографией, если не сложно, потому что напечатать такое вряд ли получится

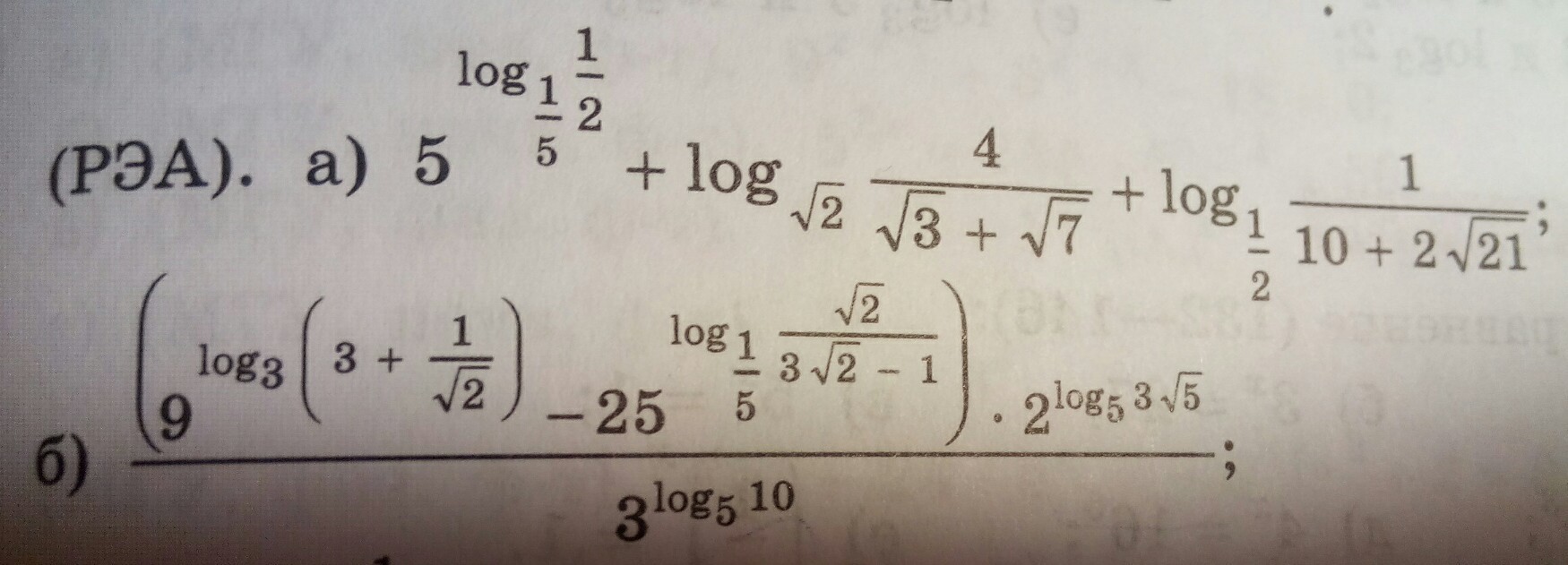
Ответы 4

а под Б можешь объяснить, что со знаменателем происходит?
- Автор:
  jasminepratt
- 4 года назад
- 0
Я же написал в решении - выделяется множитель 3, а затем сокращается с числителем
- Автор:
  navarroybo9
- 4 года назад
- 0
Можешь первое уравнение отредактировать так же красиво? а то оно не отображается как второе
- Автор:
  kaleybenton
- 4 года назад
- 0
$5^{log_\frac{1}{5}\frac{1}{2}}+log_{\sqrt{2}}{\frac{4}{\sqrt{3}+\sqrt{7}}+log_{\frac{1}{2}}{\frac{1}{10+2\sqrt{21}}=$ $5^{log_{5}{2}}+2log_{2}{4}-2log_{2}{({\sqrt{3}+\sqrt{7})}+log_{2}{({10+2\sqrt{21})}=$ $2+2*2-2log_{2}{({\sqrt{3}+\sqrt{7})}+log_{2}{({\sqrt{3}+\sqrt{7})^2}=6$ $\frac{(9^{log_3{(3+\frac{1}{\sqrt{2}})}}-25^{log_{\frac{1}{5}}{(\frac{\sqrt{2}}{3\sqrt{2}-1})}})*2^{log_5{3\sqrt{5}}}}{3^{log_5{10}}} =$ $\frac{(3^{2{log_3{(3+\frac{1}{\sqrt{2}})}}}-5^{2log_{{5}}{(3-\frac{1}{\sqrt{2}})}})*2^{log_5{3\sqrt{5}}}}{3^{1+log_5{2}}} =$ $\frac{((3+\frac{1}{\sqrt{2}})^2-{(3-\frac{1}{\sqrt{2}})^2})*2^{log_5{3+\frac{1}{2}}}}{3*3^{log_5{2}}} =$ $\frac{(6{\sqrt{2}})*\sqrt{2}*2^{log_5{3}}}{3*3^{log_5{2}}} = 4\frac{2^{log_5{3}}}{3^{log_5{2}}}=4\frac{5^{log_5{2}*log_5{3}}}{5^{log_5{3}*log_5{2}}}=4$
- Автор:
  facundogardner
- 4 года назад
- 0
Добавить свой ответ

Еще вопросы