-
найти максимальную скорость движения тела, заданного управлением
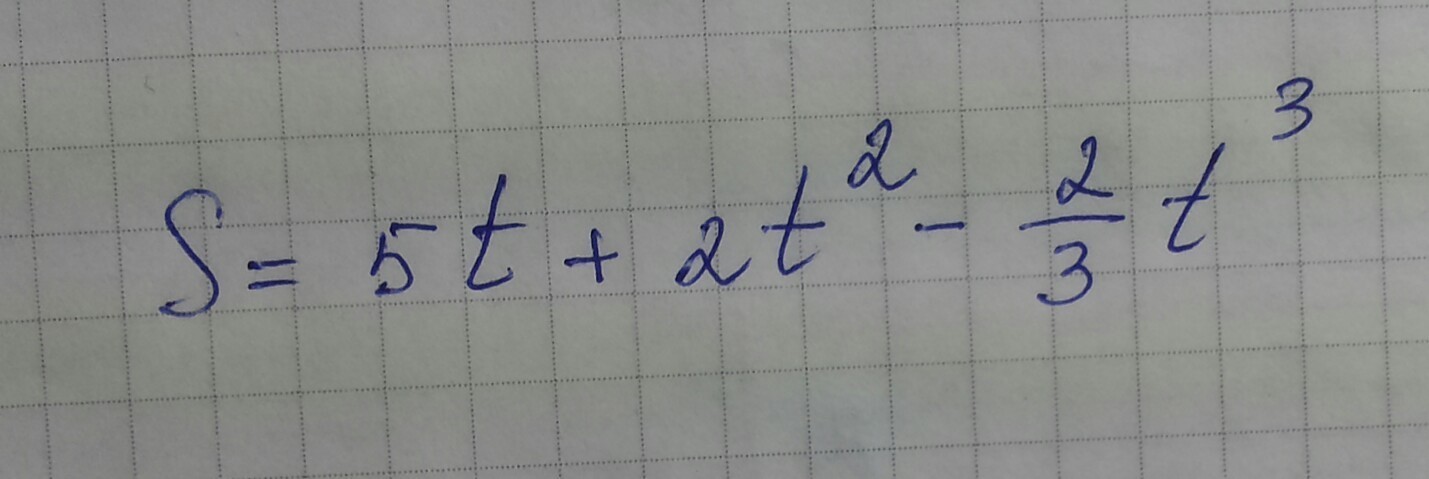
-
Предмет:
Алгебра -
Автор:
carlieblackwell - 5 лет назад
-
Ответы 2
-
спасибо большое)
-
Автор:
kenna - 5 лет назад
-
0
-
-
введём функцию
найдём производную функции:
найдём такие значения переменной, которые обращают в ноль производную:
-
Автор:
jabarityec - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Сказка Черная курица или Подземные жители.Какие Алеша сделал поступки отрицательные и положительные
-
Предмет:
Литература -
Автор:
caliczvh - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите
34052:???=34 (ост.52)
24385:???=(ост.5)
Где вопросики стоят мне нужно число-
Предмет:
Математика -
Автор:
jennyeapk - 5 лет назад
-
Ответов:
3 -
Смотреть
-
-
Помогите пж 256 упражнение
-
Предмет:
Русский язык -
Автор:
diesel0dvr - 5 лет назад
-
Ответов:
1 -
Смотреть
-
- ПОЖАЛУЙСТА помогите я случайно написала география это геометрия
How much to ban the user?
1 hour
1 day
100 years
