Задать вопрос Регистрация
Помочь другим

  • 99. Непрерывная случайная величина имеет плотность распределения f(x)=½x на отрезке X∈ [0;2]. Среднее квадратичное отклонение этой случайной величины равно:
    (Варианты ответов ниже)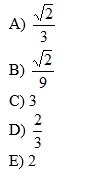

    question img

Ответы 1

  • По определению математического ожидания случ. величины Х, имеем, что                            M(X)=\displaystyle \int\limits^2_0x\cdot \frac{x}{2} dx= \frac{x^3}{6}\bigg|^2_0= \frac{4}{3} Дисперсия:       D(X)=M(X)^2-(M(X))^2=\displaystyle \int\limits^2_0x^2\cdot xdx-\bigg( \frac{4}{3} \bigg)^2= \frac{x^3}{3}\bigg|^2_0- \frac{16}{9}= \frac{2}{9} Среднее квадратичное отклонение случайной величины Х:                                 s= \sqrt{D(X)}= \dfrac{\sqrt{2}}{3}

    • Автор:

      spotblvw
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years