-
Нвйти все значения параметра а при которых уравнение имеет хотя бы один корень
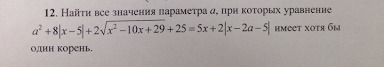
-
Предмет:
Алгебра -
Автор:
merlinricv - 5 лет назад
-
Ответы 1
-
Сделаем замену t = x - 5, тогда x = t + 5. Очевидно, у исходного уравнения и у уравнения относительно t должно быть одинаковое количество корней.
Раскроем один из модулей:
Рассмотрим правую часть уравнения из первой системы. В левой части стоит квадрат числа, так что для того, чтобы уравнение имело корни, правая часть должны быть неотрицательна. Если t < 0, то
Если t > 0, то
Итак, при t не равных нулю правая часть отрицательна, так что корней у уравнения нет. Значит, корни могут быть только при t = 0.Аналогично, и уравнение из второй системы имеет решения, только если t = 0. Поэтому если совокупность и имеет решение, то оно нулевое. Найдём, при каких a решением совокупности будет t = 0.
Ответ.
-
Автор:
dariofpsx - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
найдите периметр прямоугольника , площадь которого 28кв. см. , а одна из его сторон 7 см.
Помогите пожалуйста!-
Предмет:
Математика -
Автор:
rosy - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Составьте пожалуйста бизнес - план
-
Предмет:
Экономика -
Автор:
albertohale - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
Решите систему уравнений графическим способом {2х-3у=4 {-х+1,5у=-2
Буду благодарна пж помогитеее -
составь 5-7 больших вопросов по рассказу Николая Семёновича Лескова "Левша"
-
Предмет:
Литература -
Автор:
gustavo - 5 лет назад
-
Ответов:
8 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
