-
Найти все значения параметра а, при каждом из которых уравнение имеет три различных корня
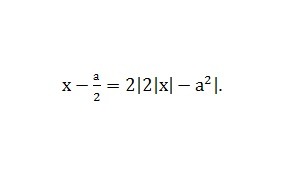
Ответы 1
-
Рассмотрим две функции вида y=x-a/2 и y=2|2|x|-a^2| . 1) линейная функция y=x-a/2 будет пересекать оси OX и OY в точка (a/2,0) и (0,-a/2) 2) функция y=2|2|x|-a^2| при x>=0 , получаем y=2|2x-a^2| откуда при x>=a^2/2 функция примет вид y=2(2x-a^2), при x3) Так как прямые коэффициенты при прямых y=x и y=4x не равны или не параллельные, тогда чтобы уравнение имело ровно три корня требуется чтобы прямая y=x-a/2 касалась другую прямую в точках либо (-a^2/2,0) либо (0,2a^2) иначе уравнение будет иметь либо два решения либо четыре. Подстановкой точек в уравнение y=x-a/2 получаем 1. 0=-a^2/2-a/2 откуда a=0 не подходит и a=-1 .2. 2a^2=-a/2 откуда a=0 подходит и a=-1/4 . Ответ a=-1 и a=-1/4 .
-
Автор:
dezi - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Объясните:что такое вынужденное существование и примеры вынужденного существования
-
Найдите в тексте имя существительное мужского рода, являющееся исторически однокоренным со словом «палица». Слово из текста выпишите в начальной форме.
(1)Люди скучают так.
(2)Заложив руки глубоко в карманы, удобно усаживаются на стуле, протягивают вперёд прижатые вместе ноги и, высоко загнув носки, делают такой вид, словно видят их впервые.
(3)Берут перо, бумагу, чернила, не спеша усаживаются за стол и пишут: «Ньюфаундленд, Ньюфаундленд, Ньюфаундленд. (4)Маня, Фаня, Таня… (5)Да здравствует Великобритания… (6)Геккель… Меккель… (7)0000000». (8)А под этим раз пятьдесят расписываются с необыкновенно размашистыми росчерками и замысловатейшими завитушками.
(9)Ложатся на кровать, заложив под голову руки, долго исследуют цветочки на обоях и, догадавшись, что над цветочками этими старался, по всей вероятности, взрослый человек, искренно думают по его адресу: «Идиот».
(10)Становятся где-нибудь на видном месте, например посреди комнаты, гордо отбрасывают назад голову, широко раскрывают объятия – точно так, как это изображено на книге Бальмонта «Будем как Солнце», и, слегка выпучив живот, подогнув колени и закрыв глаза, оглушительно зевают…
(11)Потом крестят рот, протирают пальцем глаза и, набрав в лёгкие много воздуха, выпускают его не сразу, а надув щеки и ударяя по ним ладонями: «Пвффу… Пвффу… Пвффу…»
(12)А то скучают ещё и так.
(13)Одеваются с «художественным беспорядком», идут к морю и, вперив взор в какую-нибудь точку на горизонте, говорят меланхолически:
– Жизнь – глубока и таинственна, как море. (14)Жизнь – это Сфинкс.
(15)Встречают приятеля и говорят ему с широчайшей улыбкой:
– А! Кого я вижу! (16)Сколько лет, сколько зим! (17)Как делишки?
(18)Встречают подругу, вяло обнимают её, вяло целуют и говорят:
– Катя, я вас люблю безумно, я без вас…
(19)А на вялую просьбу Кати оставить её в покое отвечают тоном ниже:
– Не верите? (20)Что ж, не надо. (21)Доказать это нельзя.
(22)А то ещё сидят в кафе, медленно глотают мороженое и, увидев польскую газету, делают удивлённые глаза и уверенно говорят:
– Э! Польская литература, знаете, какая-то… такая. (23)Без содержания.
(24)Ходят важно по улице, ритмически постукивают палкой и на мольбы нищего о подачке отвечают резонно:
– Такой здоровый – работать надо.
(25)Зато люди деятельные скучают иначе…
(26)Ходят по улицам и читают вывески, плакаты, афиши, записки на воротах о том, что сдаются квартиры, и всё это язвительно критикуют.
(27)Если же не критикуют, то поют: «Тра-ля-ля… тру-ту-ту… ди-ди-ди…» (28)Причём из языка, губ, зубов и слюны заводят во рту полный оркестр.
(29)Кроме того, для деятельных людей существуют ещё оконные стёкла, по которым можно часами барабанить пальцами, перочинные ножики, очень пригодные для вырезания или выцарапывания на подоконниках, столах, скамьях и стенах своих инициалов, а в случае надобности и полного звания с числом и годом в виде приложения; затем – брелоки, которые можно теребить сколько угодно, пуговичные петлички, в которые очень удобно протыкать поочерёдно пальцы обеих рук, и, наконец, телефон, в который, правда, пальцы протыкать излишне, но которым при умении тоже можно воспользоваться.
(30)Для тех же деятельных людей существуют также и объявления, которые можно читать нараспев; есть библиотечные книги с широкими полями, на которых можно откровенно подиспутировать с автором; есть еженедельно свежие юмористические журналы, с которыми обращаться можно и совсем запросто – можно полежать с ними на кушетке, закрыв ими лицо, и подремать, или же, свернув в трубочку, потрубить марш из «Аиды», а между тем бить мух, имеющих неосторожность отдыхать поблизости на стене.-
Предмет:
Русский язык -
Автор:
davon - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Ответьте пожалуйста.
Robert Fulton – Steamboat Inventor
By: Sue Peterson
Robert Fulton was born in Pennsylvania in 1765. He learned to read and write at home. Later, he was sent to a Quaker school for his education. Fulton showed an early interest in inventions and built a rocket for the Fourth of July when he was a teenager. Fulton enjoyed thinking about ideas for new inventions.
Fulton learned to draw as a child and excelled in art. When he finished his schooling, he worked in Philadelphia where he painted portraits and landscapes. At age 23, Fulton decided to move to England and while living there, he invented many different kinds of machines. He was very interested in how canal systems worked. Canals are deep paths of water for boats to travel through from one body of water to another. Usually they are man-made.
Fulton eventually moved to France and worked on canal systems. There, he used his talents for art and invention to design a submarine, which is a boat that can go underwater. Then he built a steamboat, a large boat that is powered by heating water to make steam which makes the paddlewheels move.
When Fulton moved back to the U.S., he took his steamboat invention and established the first steamboat service in the world on the Hudson River in New York. People paid money to travel by steamboat.
The first steamboat trip took 32 hours to cover 150 miles (240 kilometers) in 1807. That is equal to moving at about 5 miles (8 kilometers) an hour. That is as fast as a person can walk.
Robert Fulton is known as an American inventor who developed the first steamboat service to help people travel from one place to another. He is also called the “Father of Steam Navigation”.
Choose the right words to compete the sentences.
A steamboat is powered by ............................................
Robert was interested in .............................................
Robert's drawing were always ..............................
Запишите элементы на пустые поля сверху (каждый может быть использован несколько раз)
vapour.
man-made waterways.
exceptional.
a paddlewheel.
watercourses.
about machines.
-
Предмет:
Английский язык -
Автор:
haydenwatson - 6 лет назад
-
Ответов:
5 -
Смотреть
-
-
фильм Детство Горького rhfnrbq gthtcrfp
-
Предмет:
Литература -
Автор:
simeon77 - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
