Помогите найти все значения параметра а, при каждом из которых неравенство выполняется на

Помогите найти все значения параметра а, при каждом из которых неравенство выполняется на заданом промежутке.

x²-2(a²-1)x-4a²<0
0<x<1

На фото с графиком можно увидеть ответ, а лежит в промежутке (-1/√2 ; 0) объедение (0 ; 1/√2). Нужно прийти к этому ответу.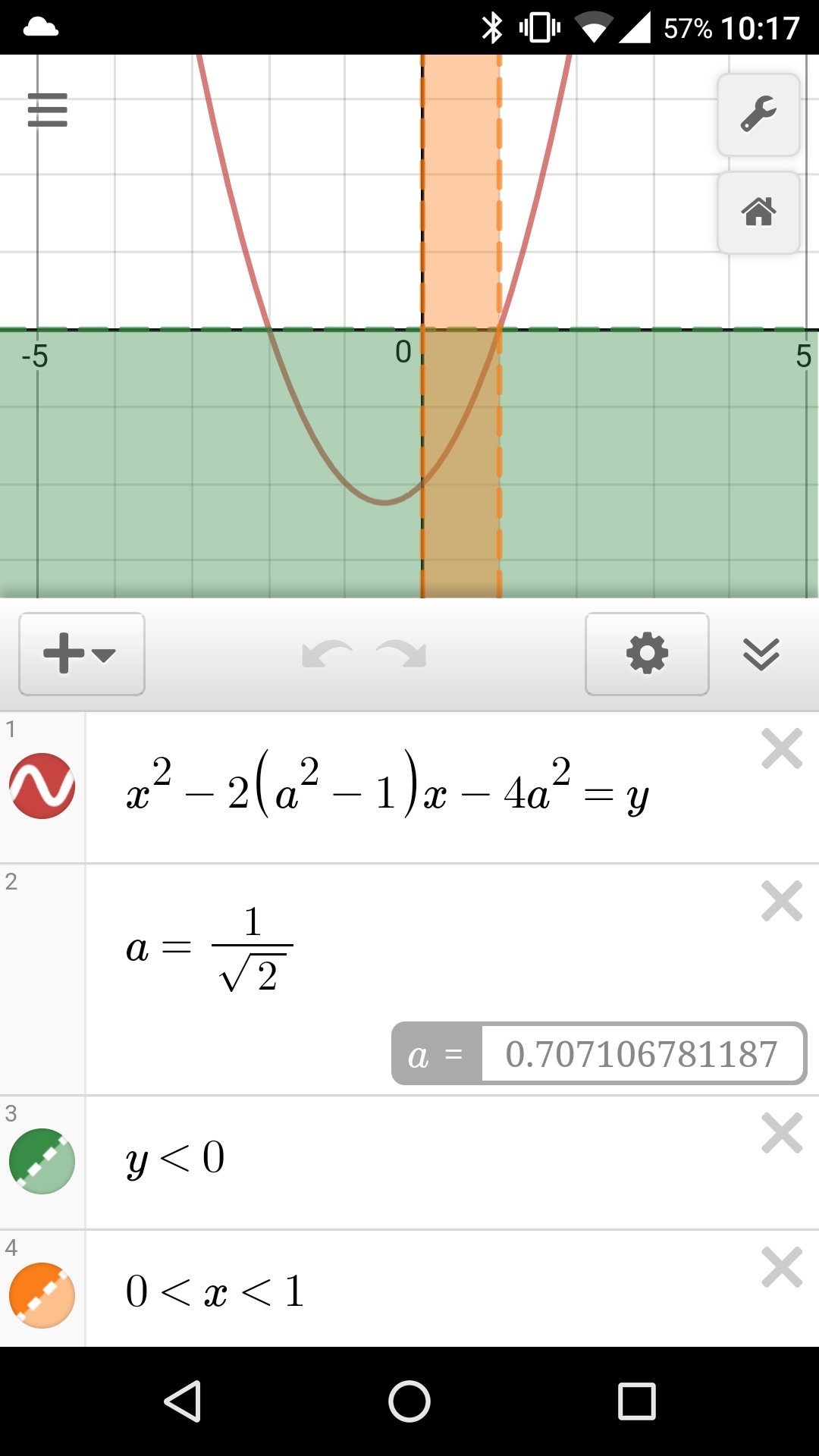
- Предмет:
  Алгебра
- Автор:
  dean7
- 5 лет назад

Ответы 5

Подскажите пожалуйста как читать ваши данные. Не понимаю на чем это написано
- Автор:
  romualdo
- 5 лет назад
- 0
Я сейчас немного поправляю
- Автор:
  tinkerbellrdvt
- 5 лет назад
- 0
Подождите еще
- Автор:
  alecfitzgerald
- 5 лет назад
- 0
спасибо
- Автор:
  clara1
- 5 лет назад
- 0
$D=4(a^2-1)^2+16a^2=4(a^4-2a^2+1+4a^2)=4(a^2+1)^2\ \textgreater \ 0$ Рассмотрим $f(x)=x^2-2(a^2-1)x-4a^2$ . Имеем параболу, ветви направлены вверх. Если дискриминант больше нуля, то решением нашей вспомогательной задачи будут те х, при которых отрезок (0;1) попадет на участок отрицательности ,т.е. выполняются следующие условия : $\displaystyle \left \{ {{f(0)\ \textless \ 0} \atop {f(1)\ \ \textless \ \ 0}} ight. ~~~\Rightarrow~~~~ \left \{ {{-4a^2\ \textless \ 0} \atop {-6a^2+3\ \ \textless \ \ 0}} ight. ~~~~\Rightarrow~~~~ \left \{ {{a\in \mathbb{R}/\{0\} \atop {a\ \textgreater \ \frac{1}{ \sqrt{2} };~~~a\ \textless \ -\frac{1}{ \sqrt{2} }} ight.$ При $a\in\bigg(-\infty;-\dfrac{1}{ \sqrt{2} }\bigg)\cup\bigg(\dfrac{1}{ \sqrt{2} };+\infty\bigg).$ решение неравенства принадлежит из 0<x<1
- Автор:
  haiden
- 5 лет назад
- 0
Добавить свой ответ

Еще вопросы

Ответы 5

Топ пользователей