Решите неравенство, с объяснением пожалуйста [tex] \frac{-23}{(x+3) ^{2}-6} \geq 0[/tex]

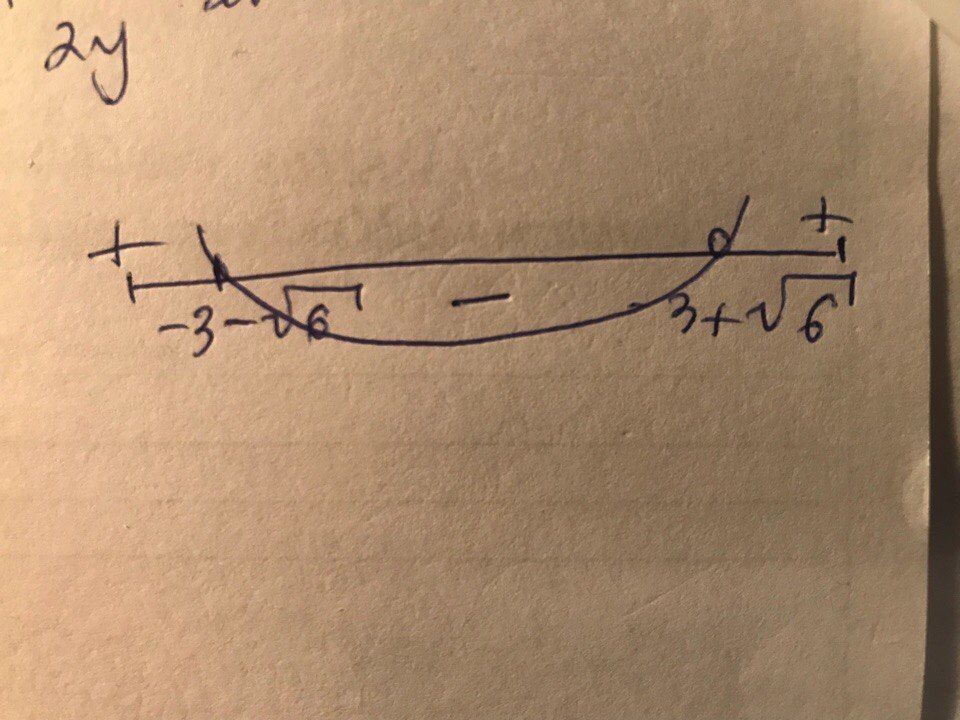
\frac{-23}{(x+3)^{2} -6}  ≥0.Т.к. числитель является числом постоянным (а именно отрицательным), то чтобы данное неравенство выполнялось нужно, чтобы знаменатель был отрицательным и не равен нулю. Т.е. (x+3)²-6<0. (x+3)²-6<0x²+6x+9-6<0x²+6x+3<0D=6²-4*3=36-12=24.x1= \frac{-6+ \sqrt{24} }{2} =-3+√6x2= \frac{-6- \sqrt{24} }{2} =-3-√6Далее чертим параболу как на рисунке. Ветви параболы направлены вверх(коэффициент при x² положителен), и проходит она через эти две точки(при чём точки выбиты, т.к. неравенство строгое). Мы можем видеть, что - будет на промежутке x∈(-3-√6;-3+√6).ОТВЕТ: x∈(-3-√6;-3+√6).