-
Решить систему уравнений, где x,y,z – комплексные числа.
x+y+z=4
x^2+y^2+z^2=18
x^3+y^3+z^3=10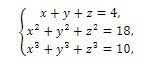
Ответы 1
-
x + y + z = 4x^2 + y^2 + z^2 = 18x^3 + y^3 + z^3 = 10xy+yz+zx = [(x+y+z)^2-(x^2+y^2+z^2)]/2 = (16-18)/2 = -1xy^2+yx^2+yz^2+zy^2+zx^2+xz^2 = (x+y+z)*(x^2+y^2+z^2) - (x^3+y^3+z^3) = 4*18 - 10 = 62xyz = [(x+y+z)^3 - (x^3+y^3+z3) - 3(xy^2+yx^2+yz^2+zy^2+zx^2+xz^2)]/6 = (64 - 10 - 186)/6 = -22x + y + z = 4 -> x+y = 4-zxy + yz + zx = -1 -> xy = -1-z(x+y) = -1-z(4-z)xyz = -22 -> z(-1-z(4-z)) = -22z^3 - 4z^2 - z + 22 = 0Можно подобрать одно из решений: z = -2, тогдаz^3 - 4z^2 - z + 22 = (z+2)(z^2-6z+11) = 0z^2 - 6z + 11 = 0z^2 - 6z + 9 = -2(z-3)^2 = -2z = 3 +- i*sqrt(2)Т.к. x,y,z входят во все уравнения симметрично, для x и y можно повторить такую же процедуру, тогдаx,y,z = {-2, 3 - i*sqrt(2), 3 + i*sqrt(2)}Причем, как видно из первого уравнения, x <> y, x <> z, y <> z
-
Автор:
butchypk9v - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Маленькое сочинение (5-10 предл) про куалу
На англ
<3
-
Предмет:
Английский язык -
Автор:
blackie25 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Помогите пожалуйста срочно!!!! Надо сочинить краткую смешную сказку!!!! Даю 15 баллов
-
Предмет:
Литература -
Автор:
joaquinxftv - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
разберите пажалуйса слово підземельний по буквам например: [Д]- твердий.,.....
-
Предмет:
Українська мова -
Автор:
jinglesbriggs - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Напишите сочинение описание действия 7 класс. Небольшое
-
Предмет:
Русский язык -
Автор:
francojttj - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
