-
70 баллов.Неопределенный интеграл(8/(x^2-2) -2/sqrt(1-4x))dx.
Пожалуйста, прошу полное решение и без ареатангенсов.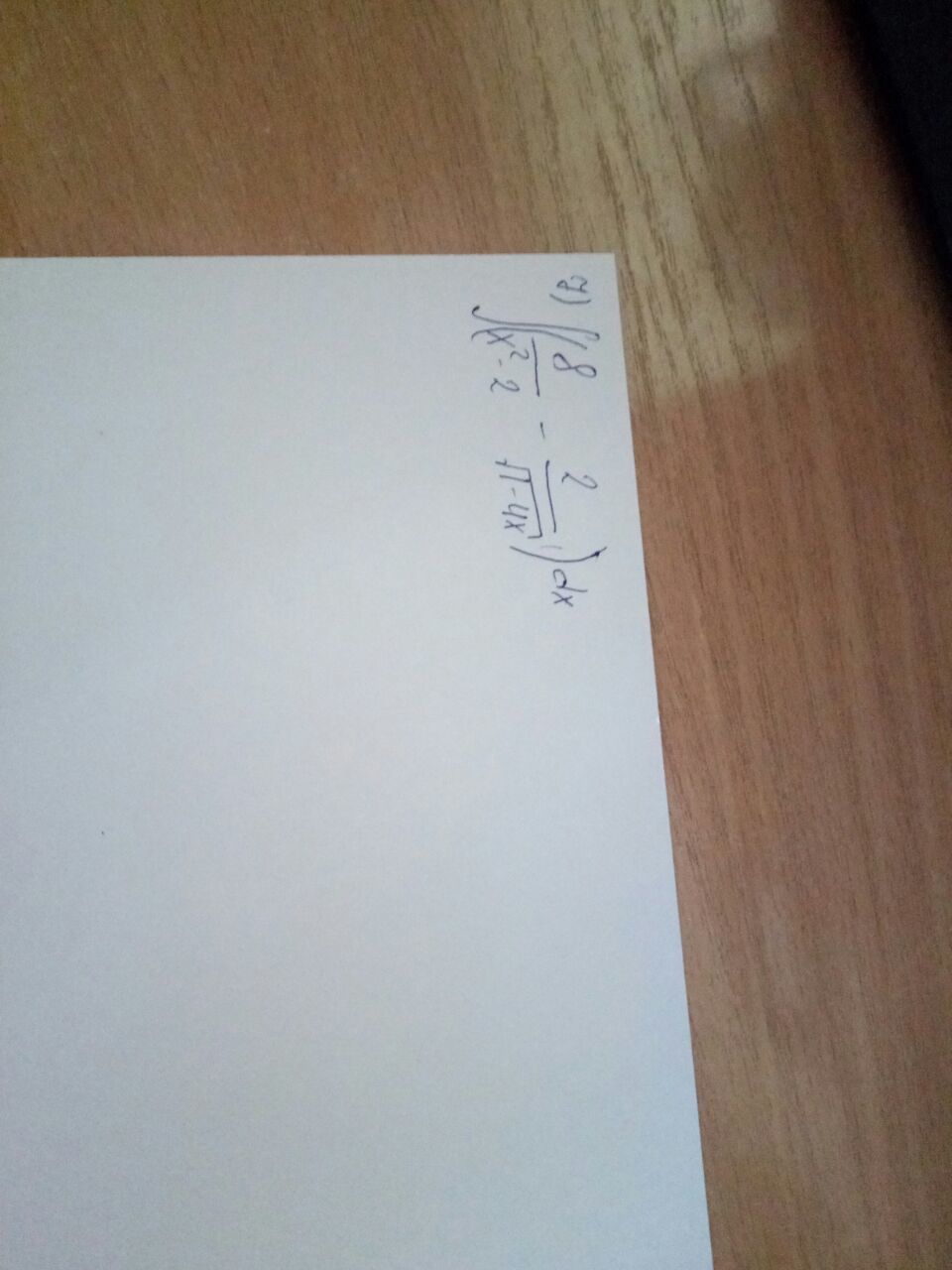
-
Предмет:
Алгебра -
Автор:
lindsayblair - 5 лет назад
-
Ответы 6
-
Можно решение? Не только ответ.
-
Автор:
marrcvb - 5 лет назад
-
0
-
-
А, там x^2 - 2. Сейчас исправлю
-
Автор:
jones - 5 лет назад
-
0
-
-
Жду.
-
Автор:
urijah - 5 лет назад
-
0
-
-
Спасибо большое!
-
Автор:
barnabybailey - 5 лет назад
-
0
-
-
-
Автор:
jabarityec - 5 лет назад
-
0
-
-
[ln|x-√2| - ln|x+√2|]' = 1/(x-√2) - 1/(x+√2) = (x+√2)/(x^2-2) - (x-√2)/(x^2-2) = 2√2/(x^2-2)[√(1-4x)]' = -4 / 2√(1-4x) = -2/√(1-4x)8/(x^2-2) - 2/√(1-4x) = 2√2 * [ 2√2/(x^2-2) ] + [ -2/√(1-4x) ]∫[ 8/(x^2-2) - 2/√(1-4x) ]dx = 2√2*[ln|x-√2| - ln|x+√2|] + √(1-4x) + C = 2√2ln( |x-√2|/|x+√2| ) + √(1-4x) + C
-
Автор:
kyra4itx - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- ежелгі мохенджо дара қаласы қалай жойылып кетті эссе
-
Choose the correct tag for each sentence. aren't they can't she won't she haven' you isn't there 1) Masha can speak English very well, ...? 2) The books are in the bookcase, ...? 3) The teacher will come at 9 o'clock, ...?4) There is a pointer on the teacher's table, ...? 5) You have got a nice classroom, ...?
-
Предмет:
Английский язык -
Автор:
tatalu2m - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
В 3 литрах сиропа содержится 1,2 кг сахара.
В x литрах сиропа содрежится 6 кг сахара.
x=
-
Предмет:
Математика -
Автор:
orr - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
где вперыве возникли религиозные движения?
-
Предмет:
История -
Автор:
vivianamccormick - 5 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
