Задать вопрос Регистрация
Помочь другим

  • Помогите пожалуйста с показательными уравнениями. Там все степени
    Просто напишите как а этих примерах выйти на простое показательное уравнение.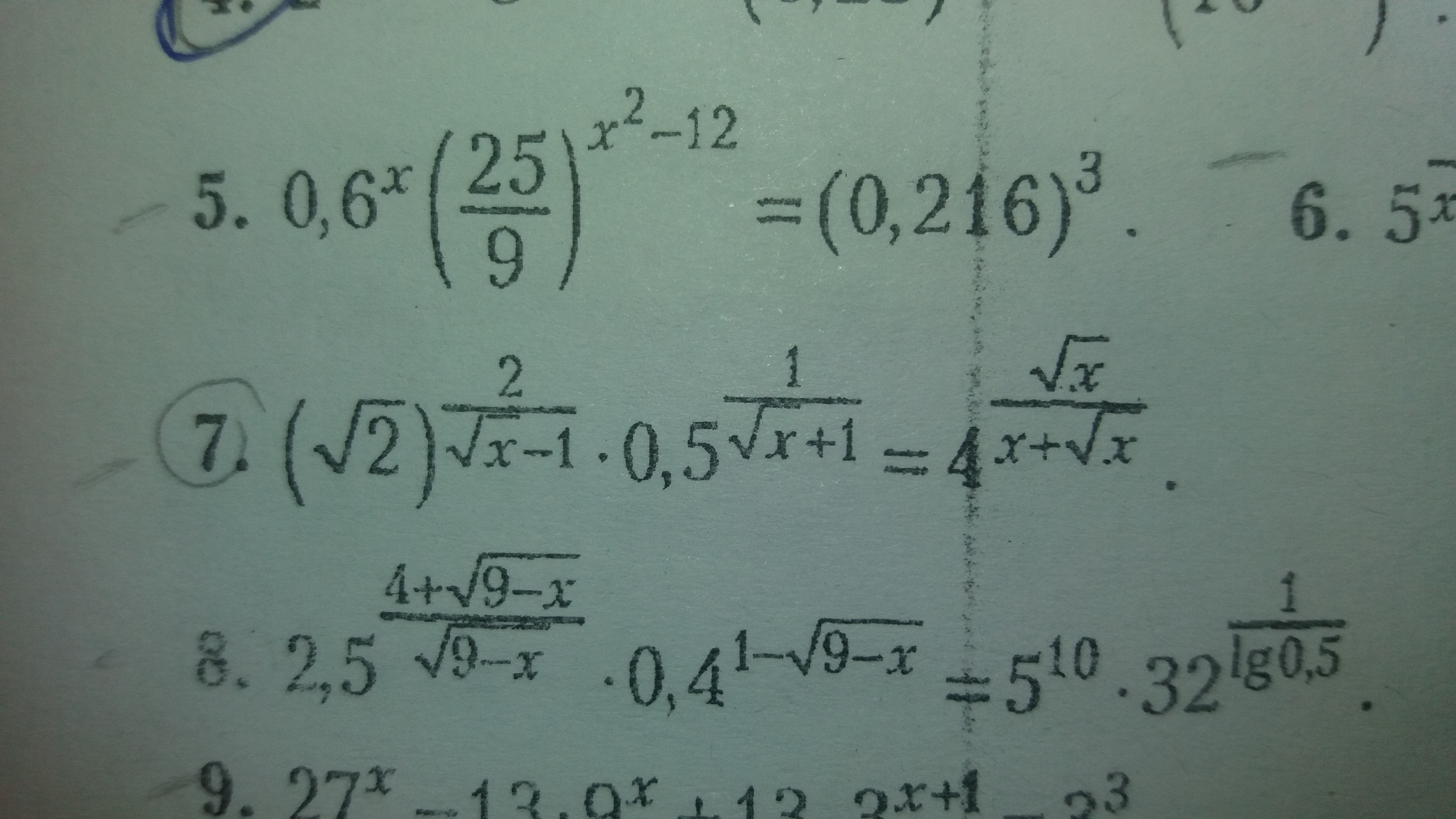

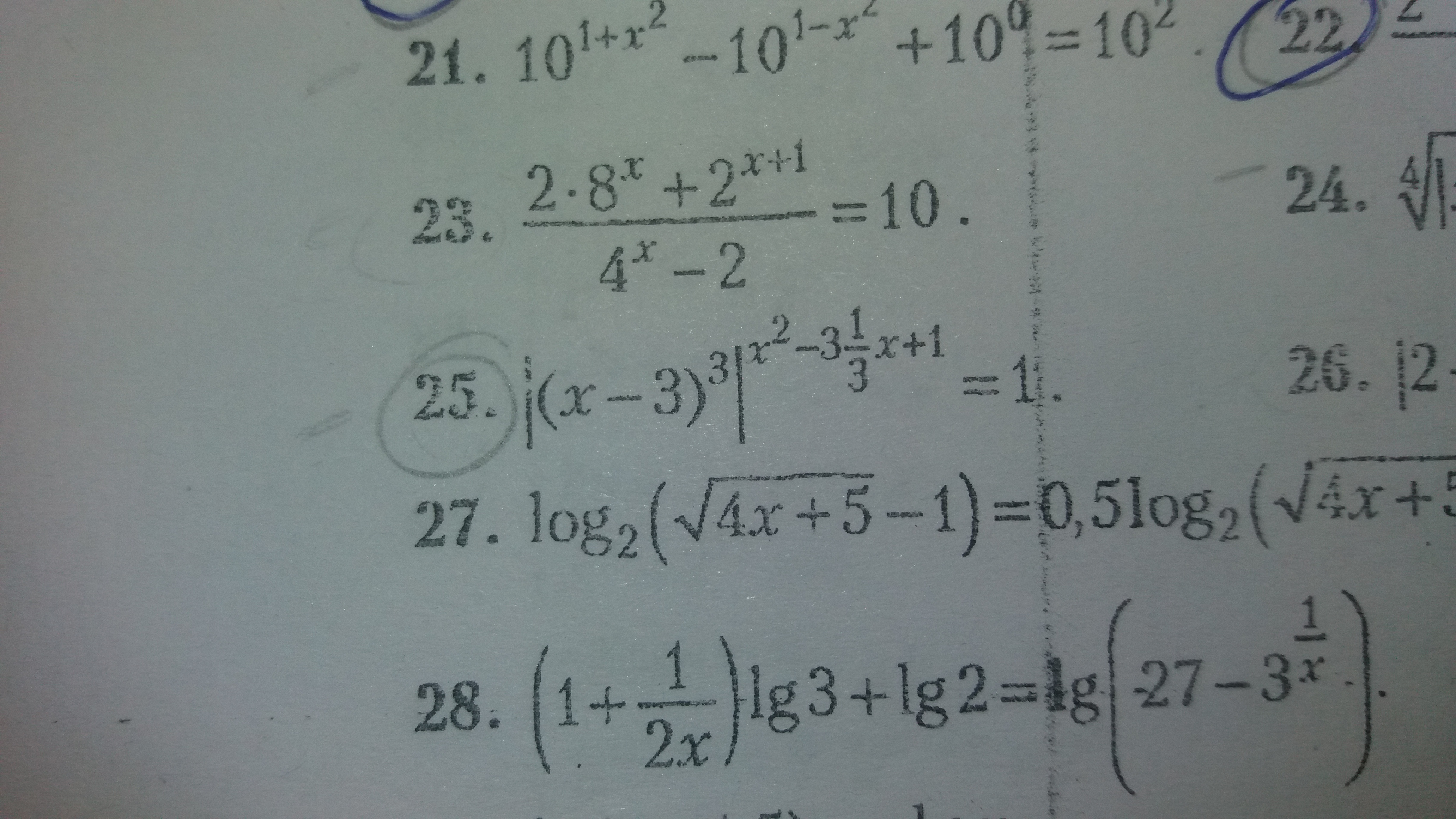
    question img
    question img
    question img

Ответы 1

  • 1) Показатель во 2 числе (-1) \frac{2+ \sqrt{x} +x}{2(1+ \sqrt{x} )} = \frac{-2- \sqrt{x} -x}{2(1+ \sqrt{x} )} Числа перемножаются, значит, показатели складываются. \frac{x}{1+ \sqrt{x} } +\frac{-2- \sqrt{x} -x}{2(1+ \sqrt{x} )} =\frac{2x-2- \sqrt{x} -x}{2(1+ \sqrt{x} )} =\frac{x- \sqrt{x} -2}{2(1+ \sqrt{x} )} Основания одинаковые, значит, и показатели равны.\frac{x- \sqrt{x} -2}{2(1+ \sqrt{x} )} =3,5= \frac{7}{2} Знаменатель 2(1 + √x) > 0 при любом x, умножаем на негоx - √x - 2 = 7(1 + √x)x - 8√x - 9 = 0(√x + 1)(√x - 9) = 0√x + 1 > 0 при любом x, поэтому корень√x = 9x = 817) Первое число слева( \sqrt{2} )^{ \frac{2}{ \sqrt{x} -1} }=2^{\frac{1}{ \sqrt{x} -1}}Второе число слева(0,5)^{\frac{1}{ \sqrt{x} +1}}=2^{\frac{-1}{ \sqrt{x} +1}}Число справа4^{\frac{ \sqrt{x} }{ x+\sqrt{x}}}=2^{\frac{2 \sqrt{x} }{ x+\sqrt{x}}}=2^{\frac{2}{ \sqrt{x} +1}}Слева умножение, значит, показатели складываются.Основания одинаковые, значит, и показатели равны.\frac{1}{ \sqrt{x} -1}+\frac{-1}{ \sqrt{x} +1}=\frac{2}{ \sqrt{x} +1}Область определения: x >= 0; x ≠ 1. Умножаем все на (√x - 1)(√x + 1) = x - 1√x + 1 - (√x - 1) = 2(√x - 1)2 = 2√x - 22√x = 4x = 425) При x = 3 левая часть равна 0, поэтому это НЕ решение.При x ≠ 3 показатель левой части равен 03(x^2 - (3 1/3)*x + 1) = 3(x^2 - 10/3*x + 1) = 03x^2 - 10x + 3 = 0 (x - 3)(3x - 1) = 0Корень x = 3 не подходит, это мы уже выяснили.x = 1/3

    • Автор:

      karlywewc
    • 4 года назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years