Задать вопрос Регистрация
Помочь другим

  • Найти неопределённый интеграл подробно , со всеми пояснениями. Результаты проверить дифференцированием

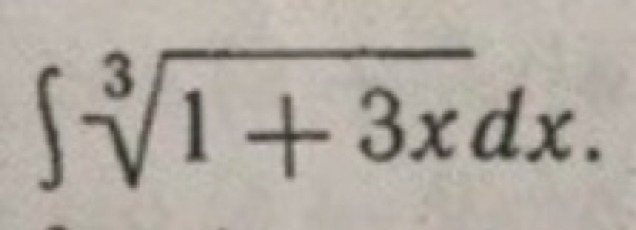
    question img

Ответы 1

  • \int\limits { \sqrt[3]{1+3x} } \, dx = \frac{1}{3} \int\limits { \sqrt[3]{1+3x} } \, d(3x) = \\ \\ = \frac{1}{3} \int\limits { \sqrt[3]{1+3x} } \, d(1+3x) = \\ \\ = \frac{1}{3} \int\limits { (1+3x)^{ \frac{1}{3} } } \, d(1+3x) = \\ \\ =\frac{1}{3} * \frac{(1+3x)^{ \frac{1}{3}+1 }}{ \frac{1}{3}+1 } +C= \frac{1}{3} * \frac{(1+3x)^{ \frac{4}{3} }}{ \frac{4}{3} } +C= \\ \\ = \frac{1}{3} * \frac{3}{4} *( \sqrt[3]{1+3x}) ^4+C= \frac{( \sqrt[3]{1+3x})^4 }{4} +CПроверка:d( \frac{( \sqrt[3]{1+3x})^4 }{4} +C)= d(\frac{1}{4} *(1+3x)^ \frac{4}{3} +C)= \\ \\ = \frac{1}{4}* \frac{4}{3}*(1+3x)^{ \frac{4}{3}-1 } *d(3x)= \frac{1}{3}*(1+3x)^ \frac{1}{3} *3*dx= \sqrt[3]{1+3x} dx

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years