Задать вопрос Регистрация
Помочь другим

  • ПОМОГИТЕ ПОЖАЛУЙСТА С ГЕОМЕТРИЕЙ!!!НУЖНО СРОЧНО!!! 303 и 304 УПРАЖНЕНИЯ.

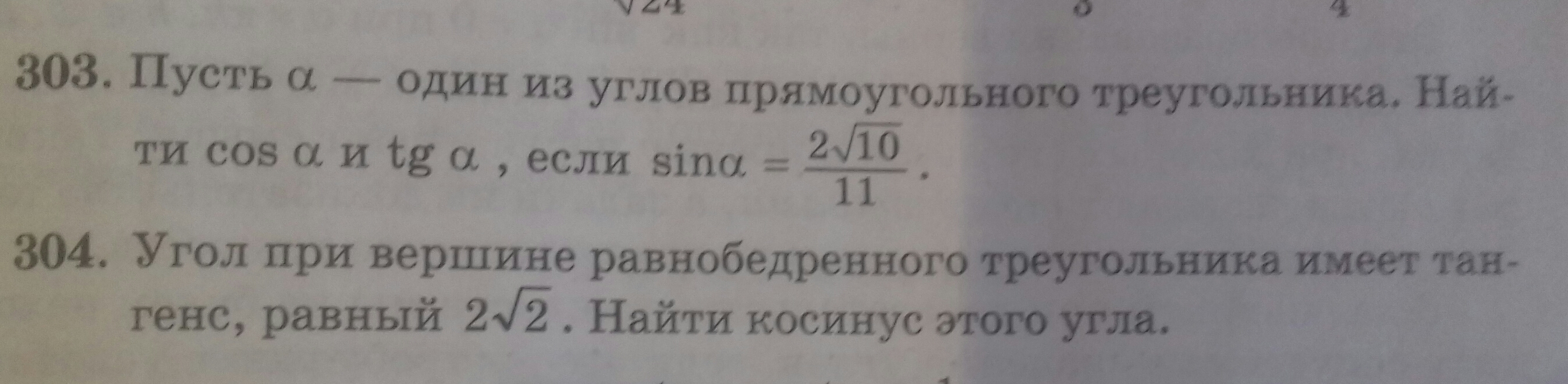
    question img

Ответы 1

  • 303у прямоугольном треугольнике один угол прямой, остальные - острые => их синусы, косинусы, тангенсы будут положительными.воспользуемся следующими формулами:sin^2\alpha+cos^2\alpha=1 \\tg\alpha= \frac{sin\alpha}{cos\alpha} применим их:cos\alpha=\sqrt{1- (\frac{2\sqrt{10}}{11})^2 }=\sqrt{1- \frac{4*10}{121} }=\sqrt{ \frac{121-40}{121} }=\sqrt{ \frac{81}{121} }= \frac{9}{11} \\tg\alpha= \frac{\frac{2\sqrt{10}}{11}}{\frac{9}{11} } = \frac{2\sqrt{10}}{9} Ответ: cos\alpha=\frac{9}{11};\ tg\alpha=\frac{2\sqrt{10}}{9}304воспользуемся следующим тождеством:tg^2\alpha+1= \frac{1}{cos^2\alpha} \\(2\sqrt{2})^2+1=\frac{1}{cos^2\alpha} \\\frac{1}{cos^2\alpha} =9 \\cos^2\alpha= \frac{1}{9} \\cos\alpha=\pm \frac{1}{3} теперь определим знак косинуса:если тангенс этого угла положительный => данный угол находится в 1 или 3 четверти. Но так как сумма углов треугольника не превышает 180°, а в 3 четверти углы от 180° до 270° - 3 четверть не подойдет, остается только 1 четверть, а в ней косинус положительный => cos\alpha= \frac{1}{3} Ответ: 1/3

    • Автор:

      bella92gg
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years