-
Решить дифференциальные уравнения(найти общее решение уравнения)80 БАЛЛОВ
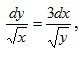
-
Предмет:
Алгебра -
Автор:
valintol1o9 - 5 лет назад
-
Ответы 1
-
Дифференциальное уравнение первого порядка с разделяющимися переменными. Всё, что относится к игрекам переносим в левую часть, что к иксам - в правую. Затем представляем в виде степенной функции, избавляясь от радикалов, чтобы применить табличный интеграл степенной функции.
На этом можно остановиться. А можно и дальше преобразовать.
Или
-
Автор:
billie41 - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- квадрат с периметром 24см вписан в окружность найдите длину дугикоторую стягивает сторона квадрата
-
Ребят)))
GUYS HELP ME PLEASE
YOU KNOW, THERE IS NO NEED
I WROTE THIS TEXT JUST
WHAT IF YOU TRANSFERRED WHEN PEREVEDITE TRANSLATION OF WRITE))))
ПЕРЕВЕДИТЕ-
Предмет:
Английский язык -
Автор:
maximus0x4c - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Весь день колеблится давлени 149/80 – 140/88. Тошнота, 4 раза рвота, сильное головокружение. Лежала в больнице. Выявлен синкоп, ВСД. Может ли моё состаяние быть связано с синкопом и ВСД? Мне 12 лет
-
Предмет:
Другие предметы -
Автор:
maggiesilva - 5 лет назад
-
Ответов:
0 -
Смотреть
-
- рассказ по Куликовской битве
How much to ban the user?
1 hour
1 day
100 years
