-
Докажите что при любом натуральном значении n выполняется равентсво:
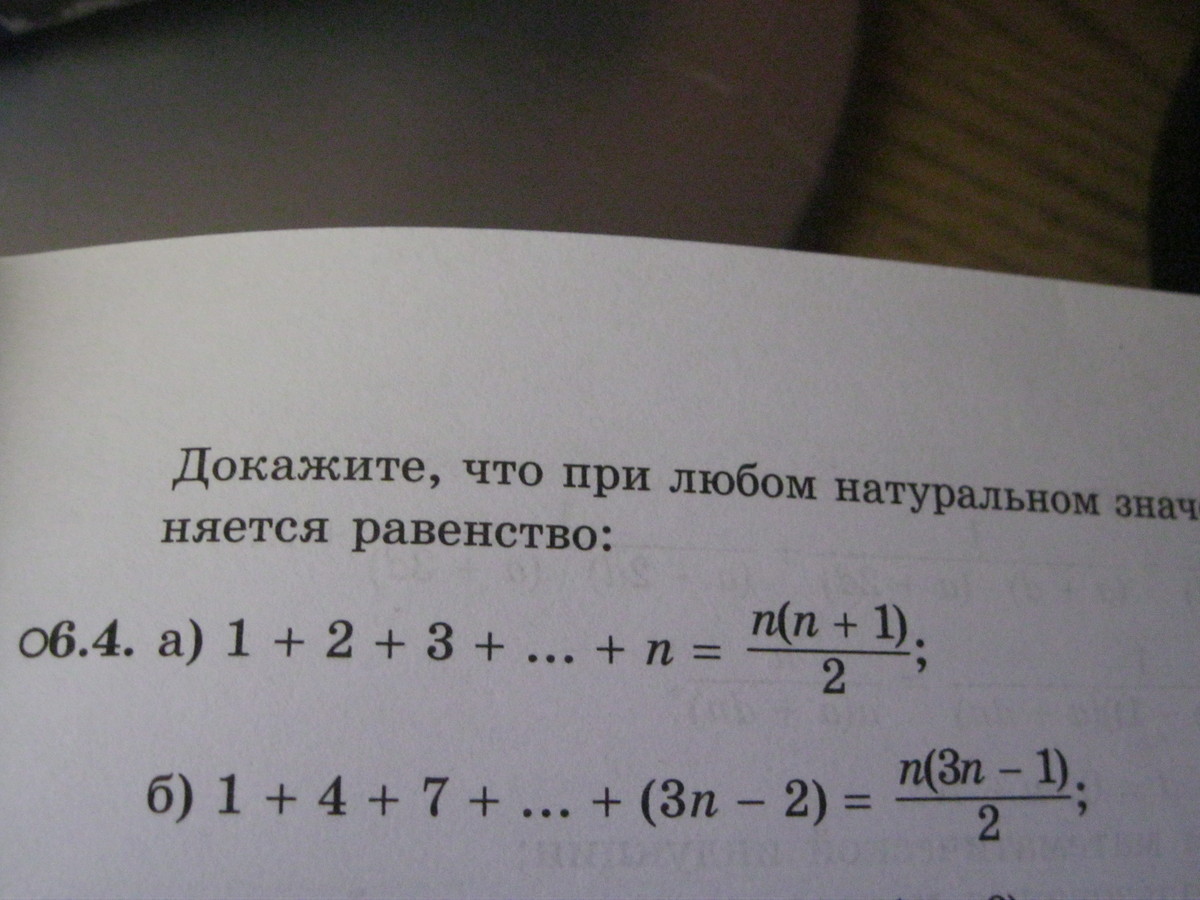
-
Предмет:
Алгебра -
Автор:
anthonydavis - 5 лет назад
-
Ответы 2
Еще вопросы
- Найдите площадь круга, вписанного в ромб с диагоналями равными 16 см и 30 см.
-
По каким признакам можно определить, что "Игра" Б. Емельянова - это рассказ? 1)Сколько эпизодов из жизни героев описано. 2)Объем. 3) Герои.
-
Предмет:
Литература -
Автор:
josephineray - 5 лет назад
-
Ответов:
1 -
Смотреть
-
- Что такое неолитическая революция? Каково её значение?
-
Для чего географы используют эти предметы:барометр, компас, термометр?
-
Предмет:
География -
Автор:
teaganf8y2 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
