Задать вопрос Регистрация
Помочь другим

  • СРОЧНО!!!!!Решите, пожалуйста❗️❗️❗️
    7^x+2-7^x+1-2*7^x>2^x/3+1+2^x/3-1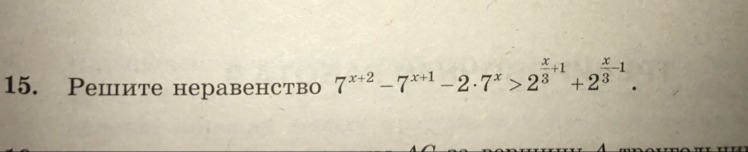

    question img

Ответы 6

  • Спасибо! Но ответ должен получиться другой :( x>-(lg 16)/(lg 7+lg 2^1/3)

    • Автор:

      meza
    • 5 лет назад
    • 0
  • мой ответ верный, сам посмотри
  • 1) Wolfram Alpha, лучший из ныне существующих решала задач https://goo.gl/QjtECD\
  • (без палки в конце)
  • и ещё Desmos "строитель" графиков https://goo.gl/hkfqJX
  • 7^{x+2}-7^{x+1}-2*7^{x}\ \textgreater \ 2^{\frac{x}{3}+1}+2^{\frac{x}{3}-1} \\ 7^{x}*7^{2}-7^{x}*7^{1}-2*7^{x}\ \textgreater \ 2^{\frac{x}{3}}*2^{1}+2^{\frac{x}{3}}*2^{-1} \\ 7^{x}*(7^{2}-7-2)\ \textgreater \ 2^{\frac{x}{3}}(2+\frac{1}{2}) \\ 7^{x}*40 \ \textgreater \ 2^{\frac{x}{3}}*\frac{5}{2} \\ 7^{x}*80 \ \textgreater \ 2^{\frac{x}{3}}*5 \\ 7^{x}*16 \ \textgreater \ 2^{\frac{x}{3}} \\ 7^{x}\ \textgreater \ \frac{2^{ \frac{x}{3}}}{16} \\ \frac{7^{x}}{2^{\frac{x}{3}}}}\ \textgreater \ \frac{1}{16} \\ (\frac{7}{2^{\frac{1}{3}}}})^x\ \textgreater \ \frac{1}{16} \\ x \ \textgreater \ log_{\frac{7}{2^{\frac{1}{3}}}}} \frac{1}{16} \\ x \ \textgreater \ \frac{ln(\frac{1}{16})}{ln{\frac{7}{2^{\frac{1}{3}}}}}} \\ x \ \textgreater \ \frac{ln(2^{-4})}{ln(7)-ln({2^{\frac{1}{3}})}}}}\\ x \ \textgreater \ \frac{-4*ln(2)}{ln(7)- \frac{1}{3} ln({2)}}\\ x \ \textgreater \ \frac{-12*ln(2) }{3*ln(7)-ln({2)}}\\ x \ \textgreater \ \frac{-12ln(2)}{3ln(7)-ln({2)}}\\ x \ \textgreater \ \frac{12ln(2)}{ln({2)-3ln(7)}}\\

    • Автор:

      chavez
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years