100 баллов. Вычислить интеграл. С подробным (!) объяснением.

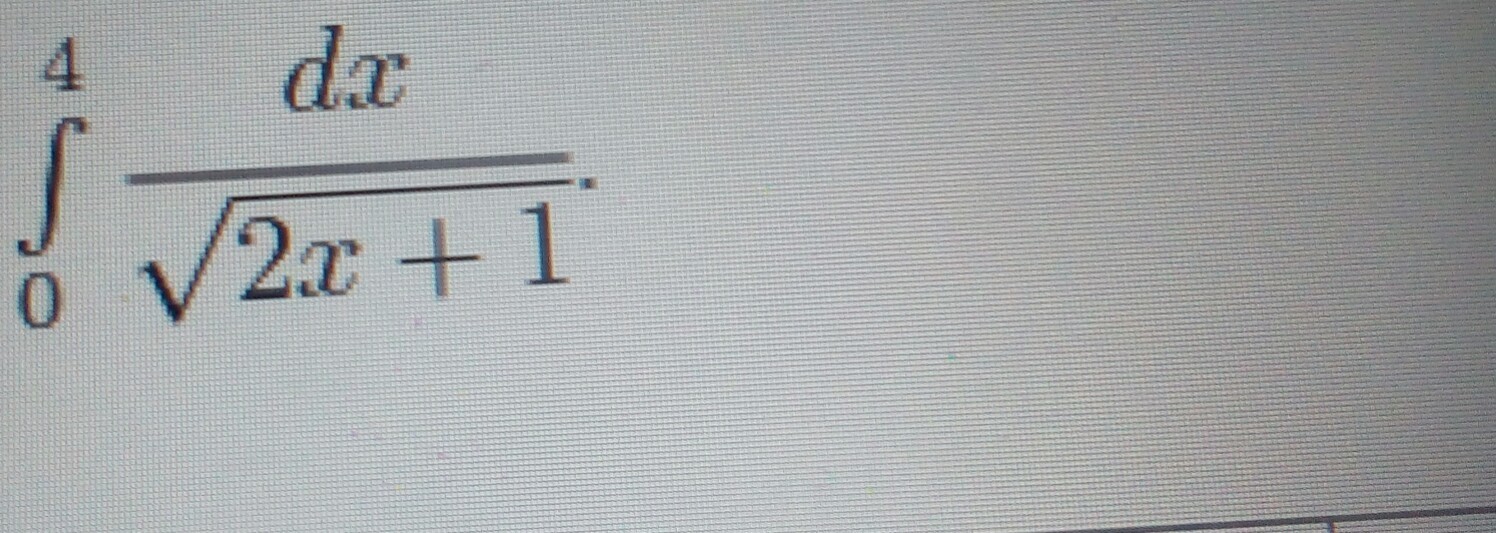
Ответы 6

А можно поподробнее, пожалуйста, этот про переход к данному равенству (2dx=du)? Как именно оно появилось? Никак не могу понять именно этот момент:(
- Автор:
  heidi97
- 5 лет назад
- 0
выделение дифферинцала
- Автор:
  georgiat6gb
- 5 лет назад
- 0
просто берем производную с обоих сторон и приписываем d
- Автор:
  roland
- 5 лет назад
- 0
точнее dx
- Автор:
  toodles5yc2
- 5 лет назад
- 0
Теперь поняла) Спасибо!
- Автор:
  baby bird7h7w
- 5 лет назад
- 0
квадратный корень - это степень 1/2, а одно из свойств степени: 1/a^n=a^(-n) $\int\limits^4_0 { \frac{1}{\sqrt{2x+1}} } \, dx = \int\limits^4_0 { \frac{1}{(2x+1)^{ \frac{1}{2} }} } \, dx = \int\limits^4_0 {(2x+1)^{- \frac{1}{2}} } \, dx$ делаем замену: $2x+1=u \\2dx=du \\dx= \frac{du}{2}$ константа выносится за знак интеграла $\frac{1}{2} \int\limits^4_0 {(u)^{- \frac{1}{2}} } \, du= \frac{1}{2} * \frac{u^{ -\frac{1}{2} +1}}{-\frac{1}{2} +1}\bigg |^{4}_{0} = \frac{1}{2} *2\sqrt{u}\bigg |^{4}_{0}=\sqrt{u}\bigg |^{4}_{0}=\sqrt{2x+1}\bigg |^{4}_{0}=\\=\sqrt{8+1}-\sqrt{1}=3-1=2$ Ответ: 2
- Автор:
  hunter19
- 5 лет назад
- 0
Добавить свой ответ

Еще вопросы