-
Самостоятельная работа по этой теме : Исследование и построение графиков функций с помощью производной
Решите пожалуйста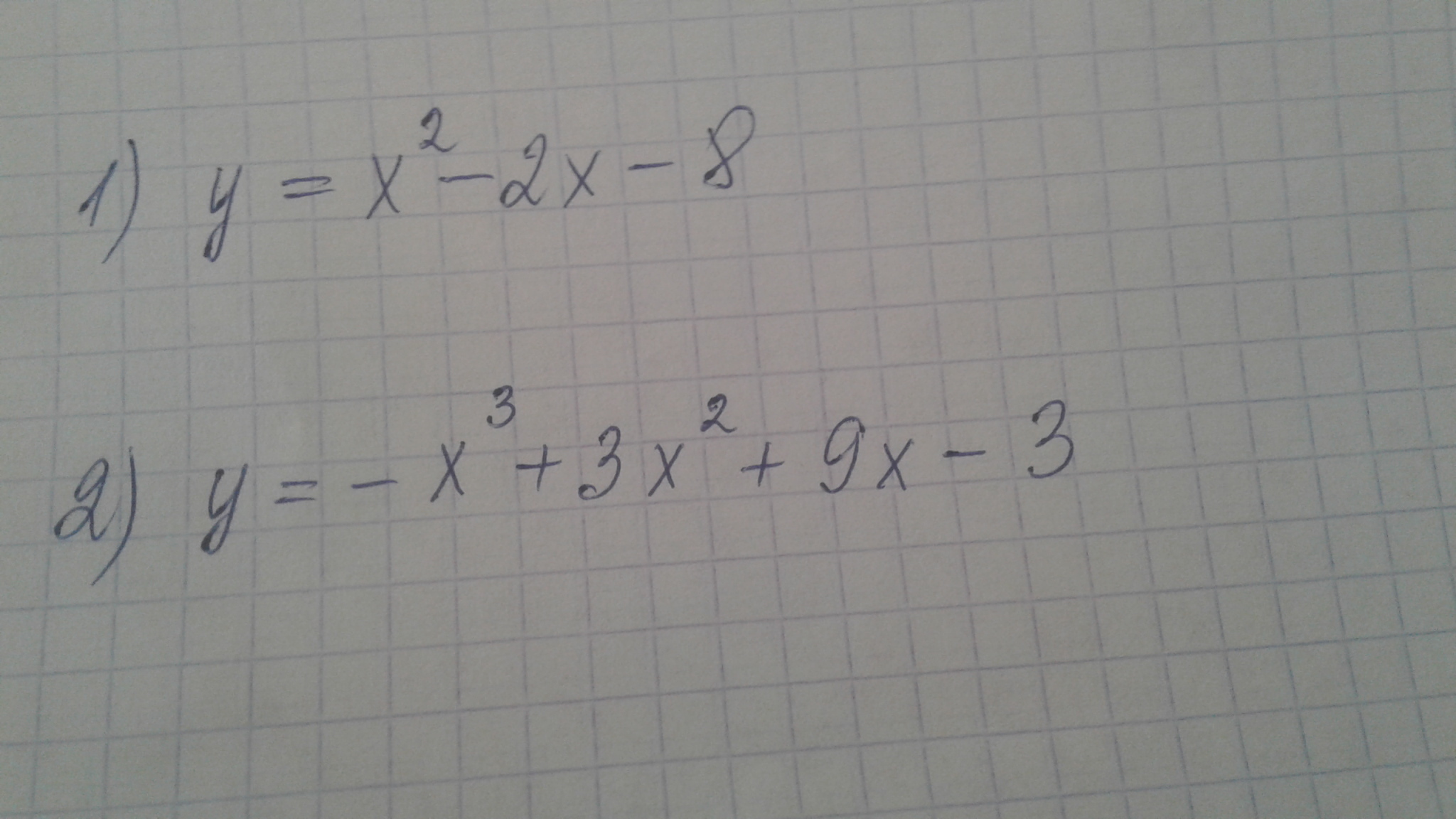
-
Предмет:
Алгебра -
Автор:
auroraonqk - 6 лет назад
-
Ответы 1
-
1) y = x^2-2x-8 - парабола, ветви направлены вверхНайдем вершину (x0;y0)x0 = -b/2a = -(-2)/2*1 = 2/2=1y0 = y(1) = -9(1;-9) - вершина параболыНайдем производнуюy' = 2x-2Найдем ее нули2x-2=0x = 1При x < 1 y' < 0 => функция убывает на промежутке (-бесконечность;1)При x > 1 y' > 0 => функция возрастает на промежутке (1;+бесконечность)Дальше нужно доп.точки взять, к примеру, найти нули самой функцииy = x^2-2x-8 = 0x1 = 4 ; x2 = -2Осталось только график построить :)2) y = -x^3+3x^2+9x-3Найдем производнуюy' = -3x^2+6x+9Найдем ее нули-3x^2+6x+9 = 0 | разделим на -3x^2-2x-3=0x1 = 3 ; x2= -1Посмотрим, как ведет себя производная в районе этих точекпри x < -1 y' < 0 => y убывает на промежутке (-бесконечность;1)при -1<x<3 y'> 0 => y возрастает на промежутке (-1;3)при x > 3 y'<0 => y убывает на промежутке (3;+бесконечность);Со 2 тоже в принципе, все, осталось только доп.точки взять и построить
-
Автор:
oliver15 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Помогите пж,реки и озера башкортостана
-
Чашка в 3 раза дороже блюдца . Блюдце дешевле чашки на 12 рублей. Сколько стоит чашка и сколько стоит блюдце?
Давно мучаюсь
Помогите плиз
42 балла-
Предмет:
Математика -
Автор:
timberritb - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Обчисліть (не використовуючи таблицю і мікрокалькулятор) sin 75°
-
Предмет:
Алгебра -
Автор:
collinvasquez - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите решить уровнение 380:(12-x)-15=23
Как нужно решить (пример)
(x:8-4)×7=35
X:8-4=35:7
X:8-4=5
X:8=5+4
X:9=9
X=8×9
X=72
Помогите пожалуйста!-
Предмет:
Математика -
Автор:
timothy38 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
