Помогите, пожалуйста, решить тригонометрическое уравнение. Подробно

Помогите, пожалуйста, решить тригонометрическое уравнение. Подробно
- Предмет:
  Алгебра
- Автор:
  manning
- 6 лет назад

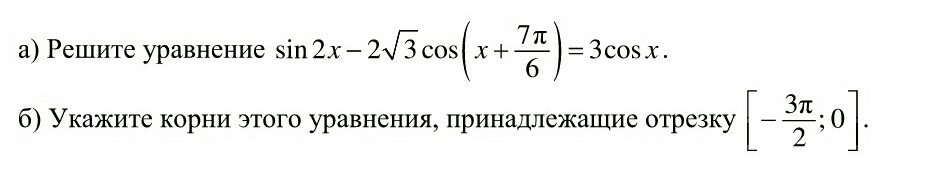
Ответы 3

Есть ещё один корень. В первой серии: n= -1 x= - pi
- Автор:
  princessthyd
- 6 лет назад
- 0
Спасибо
- Автор:
  sammyb0yf
- 6 лет назад
- 0
$\sin2x-2 \sqrt{3} \cos\left(x+ \dfrac{7 \pi }{6} ight)=3\cos x$ $\sin2x-2 \sqrt{3} \left(\cos x\cos \dfrac{7 \pi }{6} -\sin x\sin \dfrac{7 \pi }{6} ight)=3\cos x$ $\sin2x-2 \sqrt{3} \left(\cos x\cdot\left(- \dfrac{ \sqrt{3} }{2}ight) -\sin x\cdot\left(- \dfrac{ 1 }{2}ight) ight)=3\cos x$ $\sin2x-2 \sqrt{3} \left(-\dfrac{ \sqrt{3} }{2} \cos x+ \dfrac{ 1 }{2}\sin x ight)=3\cos x$ $\sin2x+3\cos x- \sqrt{3} \sin x =3\cos x$ $\sin2x- \sqrt{3} \sin x =0$ $2\sin x\cos x- \sqrt{3} \sin x =0$ $\sin x\left(2\cos x- \sqrt{3}ight) =0 \\\ \sin x=0\Rightarrow \boxed{x_1= \pi n , \ n\in Z} \\\ 2\cos x- \sqrt{3}=0\Rightarrow \cos x= \dfrac{ \sqrt{3} }{2} \Rightarrow \boxed{x_2=\pm \dfrac{ \pi }{6} +2 \pi n, \ n\in Z}$ Отбор корней.1 серия: $- \dfrac{3 \pi }{2} \leq \pi n \leq 0$ $- \dfrac{3 }{2} \leq n \leq 0$ $n=0: \ \boxed{x=0}$ $n=-1: \ \boxed{x=- \pi }$ 2 серия: $- \dfrac{3 \pi }{2} \leq \dfrac{ \pi }{6} +2 \pi n \leq 0$ $- \dfrac{3 }{2} \leq \dfrac{1 }{6} +2 n \leq 0$ $- \dfrac{3 }{2}-\dfrac{1 }{6} \leq 2 n \leq -\dfrac{1 }{6}$ $- \dfrac{5 }{4} \leq 2 n \leq -\dfrac{1 }{6}$ $- \dfrac{5 }{8} \leq n \leq -\dfrac{1 }{12}$ $notin Z$ 3 серия: $- \dfrac{3 \pi }{2} \leq -\dfrac{ \pi }{6} +2 \pi n \leq 0$ $- \dfrac{3 }{2} \leq- \dfrac{1 }{6} +2 n \leq 0$ $- \dfrac{3 }{2}+\dfrac{1 }{6} \leq 2 n \leq \dfrac{1 }{6}$ $- \dfrac{4 }{3} \leq 2 n \leq \dfrac{1 }{6}$ $- \dfrac{2 }{3} \leq n \leq \dfrac{1 }{12}$ $n=0: \ \boxed{x=-\dfrac{ \pi }{6}}$
- Автор:
  kelseyhoffman
- 6 лет назад
- 0
Добавить свой ответ