Задать вопрос Регистрация
Помочь другим

  • Составьте квадратное уравнение, корни которого удовлетворят условиям: x1 в кв. + x2 в кв. = 13; и x1 + x2 = 5(x1 - x2) ; где x1 >x2

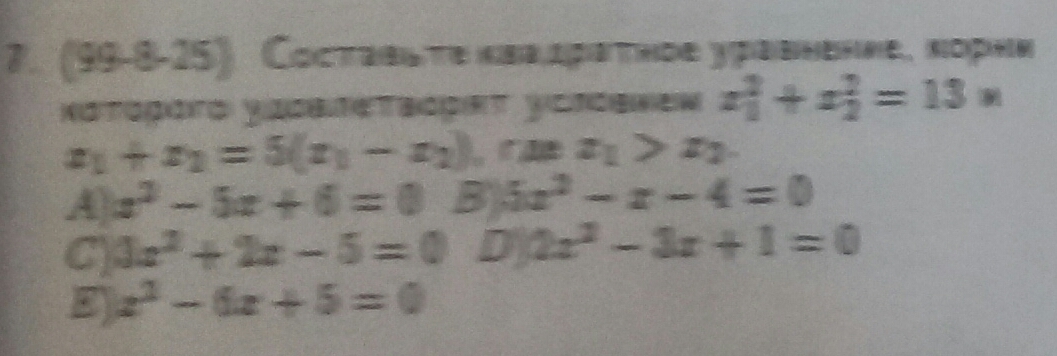
    question img

Ответы 2

  • благодарю

    • Автор:

      pineda
    • 6 лет назад
    • 0
  • x_1^2+x_2^2=13;\ 4x_1=6x_2; 2x_1=3x_2 Последнее условие выгодно переписать в виде  \left \{ {{x_1=3t} \atop {x_2=2t}} ight. , чтобы не плодить дроби. Подставляя в первое условие, получаем уравнение на t:9t^2+4t^2=13;\ 13t^2=13;\ t^2=1;\ t=\pm 1.Поскольку x_1\ \textgreater \ x_2\Rightarrow t=1; x_1=3;\ x_2=2.Остается воспользоваться теоремой Виета: если уравнение x^2+px+q=0 имеет корни x_1 и x_2, то p=-(x_1+x_2)=-5;\ q=x_1x_2=6Поэтому уравнение имеет вид x^2-5x+6=0.

    • Автор:

      buzzydisw
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years