-
Помогите решить. (Задание решается ч-з дискриминант 1 уравнения?)
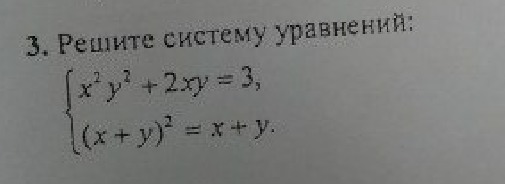
Ответы 1
-
Ответ:
-
Автор:
alejandro - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- В арифметичной прогрессии S17=187. Найти a9
- КАк вы думаете,почему Греция подченялась Македони
-
2. Выпишите номера тех предложений, в которых знаки проставлены правильно. Графически объясните постановку знаков препинания(начертить схемы тех предложений, номера которых выписали).
1. Бормочет, остывая самовар.
2. Сергей вышел, потирая руки, и, кивнув мне, уселся рядом.
3. Он остановился и, прислушиваясь к удаляющимся шагам, пошёл дальше.
4. Данко бросился вперёд, высоко держа горящее сердце, и, освещая им путь людям.
5. Ветер казавшийся слабым в лесу, в поле дул сильнее.
6. Привлечённые светом, бабочки прилетали и кружились около фонаря.
7. Она совсем измученная дорогой, не могла идти дальше.
8. Батальон, не замеченный противником, зашёл в тыл и ворвался на вокзал.
9. Тимирязев, замечательный учёный открыл законы жизни растений.
10. Под облаками, заливая воздух серебряными звуками, порхали жаворонки.
-
Предмет:
Русский язык -
Автор:
cadenjenkins - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
автопортрет Фильки из рассказа Шмыгимышь
-
Предмет:
Литература -
Автор:
emilyohs3 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
