-
При каких значениях параметра a система уравнений имеет единственное решение.
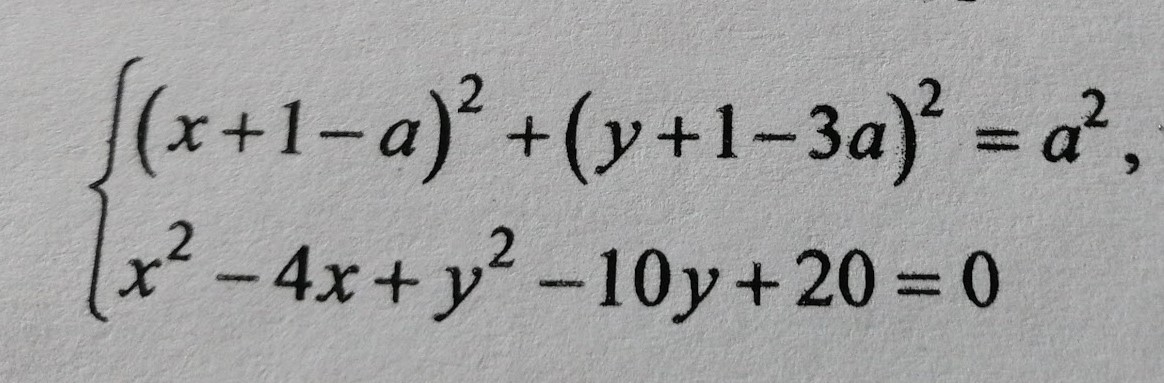
Ответы 4
-
??? Одно решение при всех этих а ???
-
Автор:
ellenmcclure - 6 лет назад
-
0
-
-
Ой, я нашел, при каких а решений нет. Сейчас исправлю.
-
Автор:
chicken wing - 6 лет назад
-
0
-
-
)) ну да - я так и понял )))
-
Автор:
generalht36 - 6 лет назад
-
0
-
-
{ (x + 1 - a)^2 + (y + 1 - 3a)^2 = a^2{ x^2 - 4x + y^2 - 10y + 20 = 0Первое - уравнение окружности с центром A(a-1; 3a-1) и радиусом R1 = а.Второе уравнение можно преобразовать так:(x^2 - 4x + 4) - 4 + (y^2 - 10y + 25) - 25 + 20 = 0Выделили полные квадраты, теперь приводим подобные:(x - 2)^2 + (y - 5)^2 - 29 + 20 = 0(x - 2)^2 + (y - 5)^2 = 9Это уравнение окружности с центром B(2, 5) и радиусом R2 = 3.Эти окружности касаются друг друга в трех случаях:1) Расстояние между центрами равно сумме радиусов.|AB| = R1 + R2
(a - 3)^2 +(3a - 6)^2 = (a + 3)^2a^2 - 6a + 9 + 9a^2 - 36a + 36 = a^2 + 6a + 99a^2 - 48a + 36 = 03a^2 - 16a + 12 = 0D/4 = 8^2 - 3*12 = 64 - 36 = 28 = (2√7)^2a1 = (8-2√7)/3; a2 = (8+2√7)/32) Окружность (В, R2) касается внутри окружности (А, R1).Тогда |AB| = R1 - R2 и R1 > R2, то есть a > 3.
(a-3)^2 + (3a-6)^2 = (a-3)^2(3a-6)^2 = 03a - 6 = 0a = 2 < 3, поэтому не подходит.3) Окружность (A, R1) находится внутри окружности (B, R2).Тогда |AB| = R2 - R1 и R1 < R2, то есть a < 3
(a-3)^2 + (3a-6)^2 = (3-a)^2(a - 3)^2 = (3 - a)^2, и, если их сократить, то получится, как в случае 2:(3a-6)^2 = 0a = 2Ответ: a1 = (8-2√7)/3); a2 = (8+2√7)/3; a3 = 2
-
Автор:
trentdtnn - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Чем можно Объяснить периодические колебания численности особей в популяциях?
-
дано точки A (-2; -2) і B (4; 6). Знайдіть координати і довжину векторів AB i BA
-
Предмет:
Геометрия -
Автор:
chasitytbgm - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Рассчитайте массу и объём (н.у.) метана,если его взято 0.25 моль
-
какой способ образования слова наказывался
-
Предмет:
Русский язык -
Автор:
kailyn - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
