-
Пожалуйста, помогите с решением системы! Буду крайне признателен!
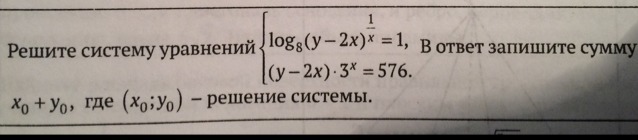
-
Предмет:
Алгебра -
Автор:
smartyhaney - 6 лет назад
-
Ответы 1
-
-
Автор:
tess - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
помогите составте слово из трех слогов
ню га дю та ма тем но
шарарам-
Предмет:
Другие предметы -
Автор:
jorgeburton - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Раскройте скобки
(не)мог,(не)сверкает,(не)годовать,(не)выходим,(не)навижу,(не)включаю,(не)пришёл,(не)волить,(не)взлюбила,(не)встречаем,(не)доумиваю,(не)здоровится,(не)белеют.-
Предмет:
Русский язык -
Автор:
simon942 - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
Корень 8*75*корень6 должно получиться 120 (решение подробно, я просто не могу понять где у меня не сходиться)
-
Предмет:
Алгебра -
Автор:
noodleskgk9 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Какую силу нужно приложить чтобы вытащить пробку из отверстия в дне бассейна. Глубина бассейна равна 4м, радиус пробки- 4см
-
Предмет:
Физика -
Автор:
lincolnperkins - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
