-
Тема производных. Найти производную, найти X, построить интервалы и выявить монотонность
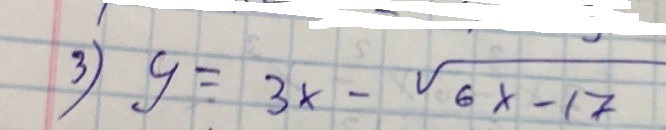
Ответы 6
-
Дерзайте ))
-
Автор:
issacacosta - 6 лет назад
-
0
-
-
а куда делась тройка в выражении, которая ещё в начале стояла? "1/ (6x -17 )^(1/2) = 1"
-
Автор:
thunder5rpi - 6 лет назад
-
0
-
-
Я перенесла ее в другую сторону и домножила на 2, после чего она превратилась в шестерку, и сократилась с шестеркой из другой части уравнения.
-
Автор:
anabellahester - 6 лет назад
-
0
-
-
Понимаете?
-
Автор:
rocky28 - 6 лет назад
-
0
-
-
Да, конечно
-
Автор:
basileo6ozg - 6 лет назад
-
0
-
-
y ' = 3 - (1/2) *((6x-17)^(-1/2)) *6 = 0 , шестерки сокращаются, после домножения на 2 , имеем : 1/ (6x -17 )^(1/2) = 1 , возводим в квадрат, перекидываем корень вправо : 6x -17 = =1 , x = 18/6 = 3. Это точка, где функция имеем экстремум. Для определения, максимум это или минимум, нужно взять вторую производную в этой точке, и посмотреть на ее знак: y'' = (1/4) * ((6x-17)^(-3/2))*6, подставляем точку x = 3, знак плюс, значит это минимум, значит слева знак минус а справа плюс, если выражаться как аутист. Вообщем это яма. Слева от этой точки функция убывает, а справа возрастает.Замечу, что у Вас стоит радикал из 6x-18, то есть фунция определена ( Это в Вашем случае, так как скорее всего Вы работаете в вещесвенной плосткости для школьников, если хотите проводить дальнейший анализ, необходимо делать аналитическое продолжение в комплексную плоскость, которое сохраняет гладкость функции, по этому оно будет единственно) при x >= 3 . Значит про то что слева от икс, Вы должны промолчать, и говорить только что справа от нее, так как слева функция не определена в вещественном смысле
-
Автор:
axelevans - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Экономические функции домохозяйства помогите пожалуйста
-
Предмет:
Обществознание -
Автор:
silly sally - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Определите и запишите основную мысль текста.
Текст 2
(1)Вышел Юрик во двор, а там мороз сразу за щёки куснул. (2)А вокруг всё в снегу: и на деревьях он лежит, и на кустах, и на заборе, и даже на проволоке, которую ещё летом натянули для гороха. (3)И такой снег аппетитный!
(4)Захотелось Юрику снежку попробовать. (5)Снял осторожно губами комочек — прохладно, как мороженое. (6)Съел первую порцию, за второй потянулся и вдруг нечаянно языком коснулся голой проволоки. (7)Язык тут же к проволоке и прилип. (8)А обожгло, как горячим чаем. (9)Не по себе стало Юрику. (10)Хотел крикнуть: «Мама!», но чтобы букву «эм» произнести, надо губы-то сомкнуть. (11)Вот они и сомкнулись... на проволоке. (12)И показалось Юрику, что он прирос к железу насовсем. (13)И от этого аж похолодело всё внутри. (14)Юрик дёрнулся, оторвался от проволоки, выплюнул снег. (15)А тот уже совсем не вкусный. (16)А во рту солёно, и щиплет, жжёт и губы, и кончик языка. (17)Заревел наш герой и бегом в дом, к маме утешаться.
(18)Мама только руками всплеснула: «Говорила же тебе столько раз: на морозе железо жжётся! (19)О чём думал-то, ворона?»
(20)То же самое Юрику и доктор объяснил, которого пригласили малыша лечить. (21)Железо не конфетка. (22)На морозе жжёт и прихватывает. (23)И маму слушать надо.-
Предмет:
Русский язык -
Автор:
chip26 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Напишите, пожалуйста, сочинение на тему «книга нас любит, но она требует и ответной любви», приводя как минимум два аргумента и соблюдая абзацы. Спасибо
-
Предмет:
Русский язык -
Автор:
romeooconnell - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Помогите найти интеграл, пожалуйста
dx/(8x-5)^7-
Предмет:
Математика -
Автор:
caliczvh - 6 лет назад
-
Ответов:
5 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
