-
В окружности. диаметр которой равен 68, проведена хорда так, что расстояние от центра окружности до этой хорды равно 30. Найдите длину этой хорды
Ответы 1
-
Дано:
Окружность с центром в т. O и D = 68. Хорда AB.
Расстояние OM = 30 от т. O до прямой AB.
Найти:AB - ?
Решение:Заметим, что OM ⊥ AB (так как OM - это расстояние от т. О до прямой AB - длина перпендикуляра из точки О к прямой AB).
Пусть отрезок OM лежит на радиусе OC рассматриваемой окружности. Тогда OC, как радиус, перпендикулярный хорде, пересекает эту хорду ровно в ее середине: AM = BM.
Рассмотрим прямоугольные треугольники, равные по первому признаку (или же по двум катетам OM = OM и AM = BM): ΔAOM = ΔBOM.
OA = OB = D / 2 = 68 / 2 = 34, как радиусы.
OM = 30, по условию.
Применим теорему Пифагора, например, к ΔAOM:
AM² + OM² = AO²
AM² = AO² - OM²
AM² = 34² - 30²
AM² = 256
AM = 16
Значит:
AB = AM + BM = AM + AM = 16 + 16 = 32.
Задача решена!
Ответ: 32.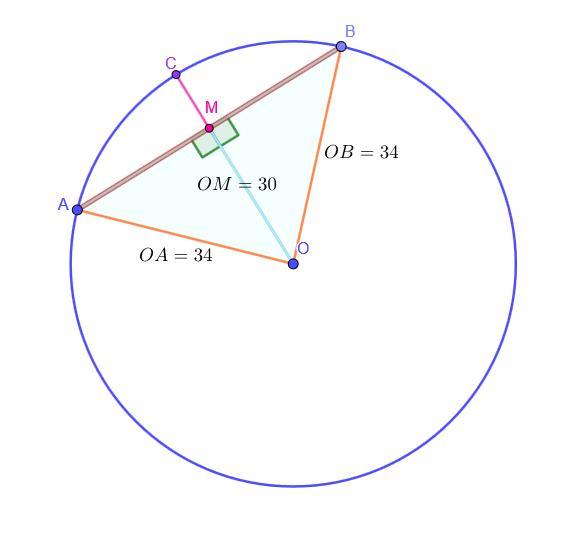
-
Автор:
olivecase - 2 года назад
-
10
-
-
Добавить свой ответ
-
В государстве инков была сооружена замечательная система дорог , которая местами используется и сейчас. особенности этих дорог- а асфальтное покрытие б абсолютная прямизна в бетонное покрытие г многочисленные участки со ступеньками помогите дам 20 баллов
-
Предмет:
Окружающий мир -
Автор:
freewaygsva - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Чим новела як літературний жанр відрізняється від оповідання й повісті (7класс) укр літ
-
Предмет:
Українська література -
Автор:
gustavoperkins - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
реферат на тему материк африка по природоведенью 4 класс
Помогите пж
Зарание спасибо
-
Предмет:
Другие предметы -
Автор:
consuelo - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
0,48-0,5+23,46:2,3-4,4:10
-
Предмет:
Математика -
Автор:
blake83 - 6 лет назад
-
Ответов:
6 -
Смотреть
-
