Задать вопрос Регистрация
Помочь другим

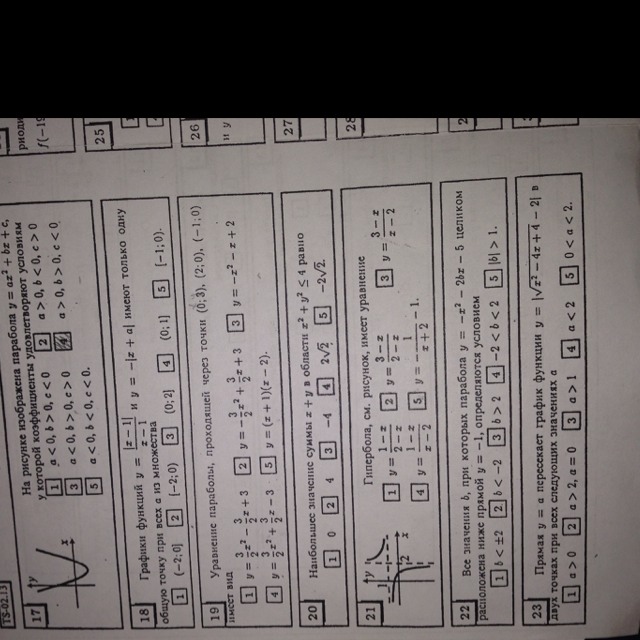
  • Решите,что можете.Только с решением,и желательно объяснением.Спасибо.

    question img

Ответы 1

  • как вы сказали какую хотите, решу  20 Можно решить 2 способами 1) x^2+y^2 \leq 4\\ применим неравенство x^2+y^2 \geq 2xy\\ так как неравенство нестрогое то применимо такое тождество2xy \leq x^2+y^2 \leq 4\\ 2xy \leq 4\\ xy \leq 4оно выполняется когда x=y\\ x=y=\sqrt{2}\\ x+y=2\sqrt{2}2) Неравенство нестрогое то   y \leq \sqrt{4-x^2}\\ x+y= x+\sqrt{4-x^2}\\ f(a)=x+\sqrt{4-x^2}\\ f'(a)=1-\frac{x}{\sqrt{4-x^2}}\\ f'(a)=0\\ x=\sqrt{2}\\  следовательно f(max)=2√2

    • Автор:

      daisycxtr
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years