Решить неравенство, изобразить решение неравенства на числовой прямой и записать ответ с помощью обозначений:

1)4х/8-х меньше или равно 0
2)2х-1/5-3х больше 10х+1/5
3)(х+6)(3х-8)-3(х^2-1) меньше 20

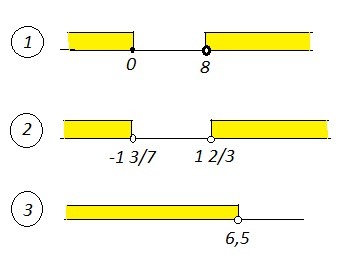
1)\; \; \frac{4x}{8-x}\leq 0\; \; \to \; \; \frac{4x}{x-8}\geq 0\\\\+++[\, 0\, ]---(8)+++\qquad x\in (-\infty ,0\, ]\cup (8,+\infty )\\\\2)\; \; \frac{2x-1}{5-3x}\ \textgreater \ \frac{10x+1}{5}\; \; \to \; \; \frac{2x-1}{5-3x}-\frac{10x+1}{5}\ \textgreater \ 0\; ,\; \; \frac{10x-5-50x-5+30x+3x}{5(5-3x)}\ \textgreater \ 0\\\\\frac{-7x-10}{5(5-3x)}\ \textgreater \ 0\; ,\; \; \frac{-(7x+10)}{-5(3x-5)}\ \textgreater \ 0\; ,\; \; \frac{7x+10}{5(3x-5)}\ \textgreater \ 0\\\\+++(-\frac{10}{7})---(\frac{5}{3})+++\\\\x\in (-\infty ,-1\frac{3}{7})\cup (1\frac{2}{3},+\infty )3)\; \; (x+6)(3x-8)-3(x^2-1)\ \textless \ 20\\\\3x^2-8x+18x-48-3x^2+3\ \textless \ 20\\\\10x\ \textless \ 65\\\\x\ \textless \ 6,5\\\\x\in (-\infty ;\, 6,5)