-
Выполнить действия
Подробное решение 10 балов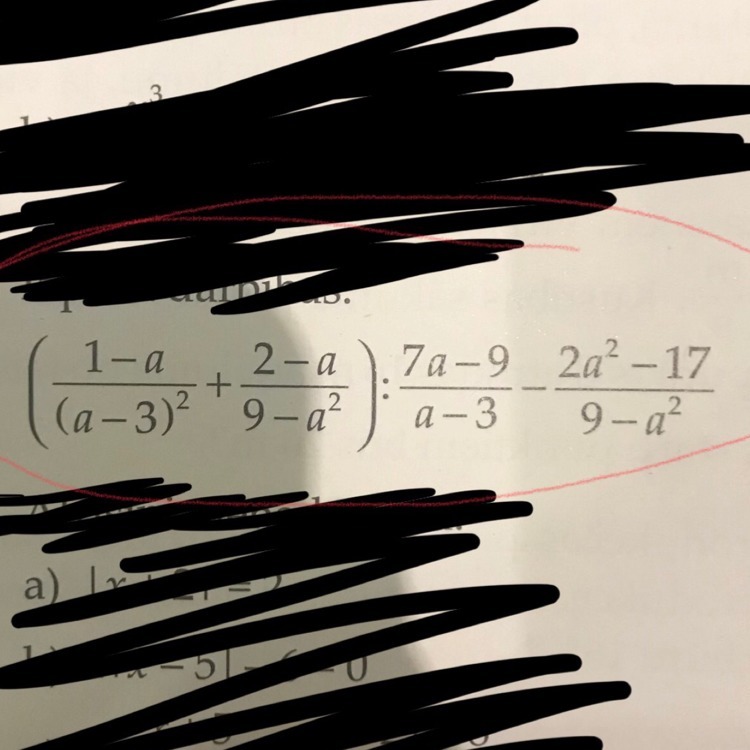
-
Предмет:
Алгебра -
Автор:
octaviokbe6 - 6 лет назад
-
Ответы 1
-
-
Автор:
lilly - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
1) x+7*4=40 2) 80-x=8*5 3) 12+x+5*8 4) x-32:4-=50 5) x+2*6=94 Помогите пожаалуйста
-
Предмет:
Математика -
Автор:
hilariónjvb3 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Решите задачу, чтоб в ответе подучилось 300см в квадрате или 0,03м в квадрате
-
Предмет:
Геометрия -
Автор:
pigletmayer - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
масса восьми одинаковых коробок с конфетами 72 кг.Масса конфет в одной коробке равна 8кг600грамм. чему равна масса пустой коробки?
помогите прошу!!!-
Предмет:
Математика -
Автор:
hailieeze8 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Помогите пжт
(51,32+x)*0,12=72
-
Предмет:
Математика -
Автор:
green giant - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
