Очень прошу помочь, не понимаю тему!!! Много баллов за один пример!!!

Очень прошу помочь, не понимаю тему!!! Много баллов за один пример!!!
- Предмет:
  Алгебра
- Автор:
  mojo
- 6 лет назад

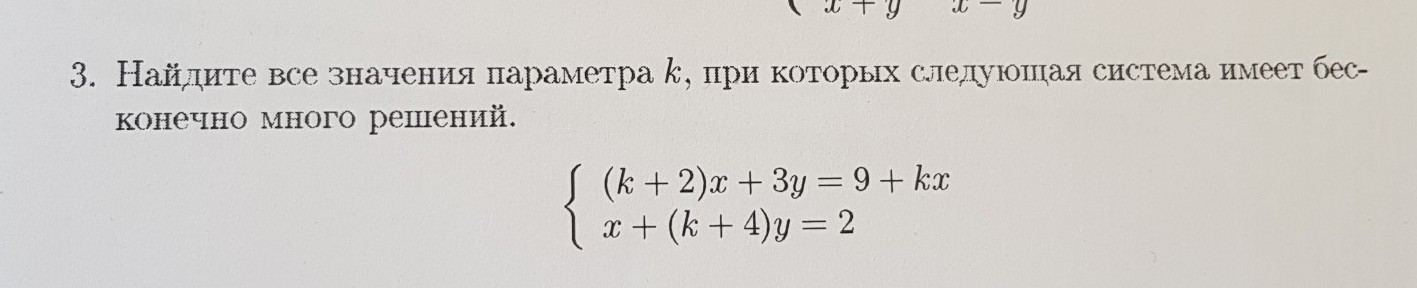
Ответы 6

2k+5
- Автор:
  miss piggyqomg
- 6 лет назад
- 0
при условии k=-2.5
- Автор:
  gilbertxosp
- 6 лет назад
- 0
тогда система выглядит как: 2x+3y-9=0 и x+1.5y-2=0
- Автор:
  bongomurray
- 6 лет назад
- 0
или как 2x+3y-9=0 и 2x+3y-4=0 - эти прямые, конечно же параллельны
- Автор:
  frau fraummrv
- 6 лет назад
- 0
т.е. СЛАУ решений не имеет
- Автор:
  velerio
- 6 лет назад
- 0
$y(x)=kx+b$ - график - прямая линия, коэффициент $k$ задает угол наклона этой линии к оси OXкоэффициент $b$ поднимает / опускает график (параллельным переносом) вдоль оси ОУесли есть две прямые: $y_1(x)=k_1x+b_1\\\\ y_2(x)=k_2x+b_2$ ,если у этих двух прямых коэффициенты равны $k_1=k_2$ , то это означает, что углы наклона к оси OX у этих прямых совпадаю, из чего следует, что эти две прямые либо параллельны либо накладываються.если дополнительно потребовать, что бы $b_1=b_2$ , то прямые $y_1$ и $y_2$ будут не просто параллельны, а будут обязательно накладываться, что будет означать что система уравнений $\left \{ {{y=k_1x+b_1} \atop {y=k_2x+b_2}} ight.$ иметь бесконечное количество решений---------------------------прямая линия задана уравненим: $ax+by+c=0$ , если $b eq$ , то $by=-ax-c\\\\ y=-\frac{a}{b}x-\frac{c}{b}\\\\ y=k'x+b'$ где $k'=-\frac{a}{b}\\\\ b'=-\frac{c}{b}$ это означает, что система уравнений: $\left \{ {{a_1x+b_1y+c_1=0} \atop {a_2x+b_2y+c_2=0}} ight.$ будет иметь бессконечное количество решений при выполнении системы условий: $\left \{ {{\frac{a_1}{b_1}=\frac{a_2}{b_2}} \atop {\frac{c_1}{b_1}=\frac{c_2}{b_2}}} ight. \\\\ \left \{ {{\frac{a_1}{a_2}=\frac{b_1}{b_2}} \atop {\frac{c_1}{c_2}=\frac{b_1}{b_2}}} ight. \\\\ {\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$ -------------------------------------- $\left \{ {{(k+2)x+3y=9+kx} \atop {x+(k+4)y=2}} ight. \\\\ \left \{ {{(k+2)x-kx+3y-9=0} \atop {x+(k+4)y-2=0}} ight. \\\\ \left \{ {{(k+2-k)x+3y-9=0} \atop {x+(k+4)y-2=0}} ight. \\\\ \left \{ {{2*x+3*y-9=0} \atop {1*x+(k+4)*y-2=0}} ight. \\\\$ необходимое и достаточное условие $\frac{2}{1}=\frac{3}{k+4}=\frac{-9}{-2}$ для параллельности прямых не выполняеться, по скольку $\frac{2}{1}eq \frac{-9}{-2}$ ------------------------------Ответ: таких значений для $k$ не существует, что бы указанная система имела бесконечное количество решений
- Автор:
  isaiahtvg9
- 6 лет назад
- 0
Добавить свой ответ