-
Вариант I
Дано: CAB = 42°.
Найти: ACO.
2. В треугольнике MNK биссектрисы пересекаются в точке О. Расстояние от точки О до стороны MN = 6 см, NK = 10 см. Найдите площадь треугольника NOK.
Вариант II
Найти: расстояние от точки О до стороны АС.
2. В треугольнике MNK медианы МР и NE пересекаются в точке О
и равны 12 и 15 см соответственно. Найдите площадь треугольника МОЕ, если МР NE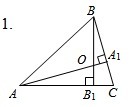
Ответы 2
-
спс
-
Автор:
eugeniohhhh - 6 лет назад
-
0
-
-
Касательно первого варианта... 1) Построим высоту СС1. Она проходит через т.О, т.к. все высоты тр-ка пересекаются в одной точке.Треугольник СС1А- прямоугольный(СС1- высота).Следовательно, угол С1АС+угол АСС1=90°.Угол АСС1=90°-42°=48°2)Точка пересечения биссектрис - центр вписанной окружности. Пусть высота от т.О к стороне MN - ОН. Т.к. МN - касательная к ОН (ОН - высота), то ОН - радиус впис.окружности. Радиусы равны и перпендикулярны сторонам тр-ка, поэтому проводим из т.О высоту к NK. S(тр-ка NOK)=h*NK/2=6*10/2=30
-
Автор:
brandysimpson - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
построить треугольник по стороне и двум прилежащим к ней углам
пожалуйста памогите и обясните как вы её решили пожалуйста-
Предмет:
Геометрия -
Автор:
kareemolit - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Синтаксический разбор со схемой и с характеристикой предложения такое птицы разыскивали в почерневший листве желуди и орехи
-
Предмет:
Русский язык -
Автор:
vancenielsen - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Найдите значение выражения (2+с)квадрате -с(с-4) при с=-1 дробная черта 8
-
Предмет:
Математика -
Автор:
pierceroman - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Переведите плиз
Я не хочу изучать эти места.
Во первых у меня нету оборудования.
Во вторых у меня нету опыта в изучении подводных глубин.
Но и для меня это просто не интересно.
Я думаю изучать дно можно возле бермудского треугольника.
Я уверен что там можно найти что-то интересное.
Раньше туда поплыть было очень сложно.
Не было оборудования и опыта.
Сейчас есть крутое оборудование.
Например батискаф , c ним можно погружаться на глубину более чем 700 метров.
Есть натренированные люди которые могут выдержать давление под водой.
Раньше было почти не возможно изучать дно а сейчас любой человек спокойно может опустится на глубина 200 метров ,но конечно с оборудованием.-
Предмет:
Английский язык -
Автор:
buddy - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
