Исследуйте функцию y=2x^3 - 3x^2 на монотонность и экстремумы. Постройте график этой функции.

Исследуйте функцию y=2x^3 - 3x^2 на монотонность и экстремумы. Постройте график этой функции.
- Предмет:
  Алгебра
- Автор:
  potter3
- 6 лет назад

Ответы 1

$y(x)=2x^3-3x^2$ $D(y):=(-\infty;+\infty)$ ищем критические точки: $y'=(2x^3-3x^2)'=6x^2-6x=6x(x-1)=0\\\\ 6x^2-6x=0\\\\ x^2-x=0\\\\ x(x-1)=0\\\\ x=0\ \ or\ \ x=1$ смотрим, как ведет себя производная функции при переходе через эти точки: $+++++++[0]---------[1]+++++++\ \textgreater \ x$ производная в точке 0 меняет знак с + на - , что означает, что точка $0$ являеться максимумом функции $y(x)$ ,производная в точке 1 меняет знак с - на + , что означает, что точка $1$ являеться минимумом функции $y(x)$ ----------------тогда промежутки монотонности:ф-ия $y(x)$ монотонно растет на промежутке $(-\infty;0)\cup(1;+\infty)$ ф-ия $y(x)$ монотонно убывает на промежутке $(0;1)$ ----------------ф-ия $y(x)$ пересекает ось ОХ в точкаx $(0;\ 0),\ (1.5;\ 0)$ $2x^3-3x^2=0\\\\ 2*x^2*(x-1.5)=0\\\\ x=0\ \ or\ \ x=1.5$ ф-ия $y(x)$ пересекает ось ОУ в точке $(0;\ 0)$ 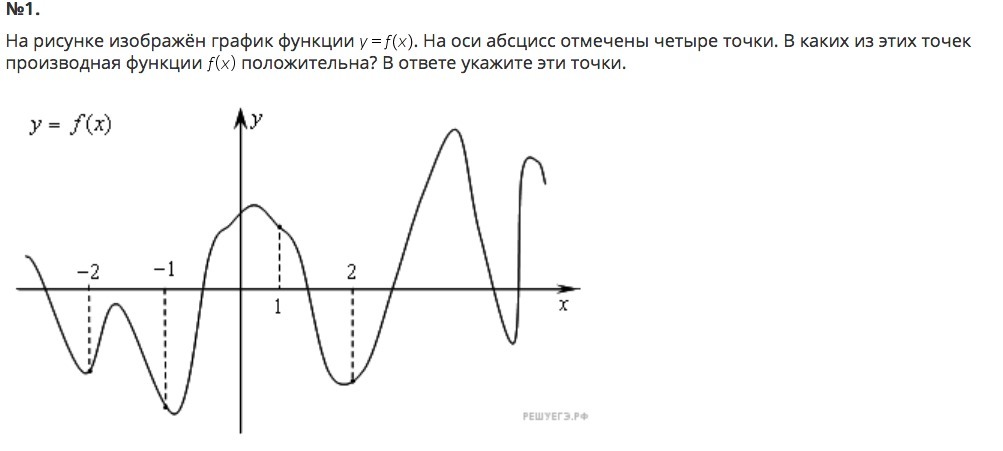на основании этих данных и строиться схематический график-------------------------------#1 производная функции положительна в точках $-2;\ 2$ (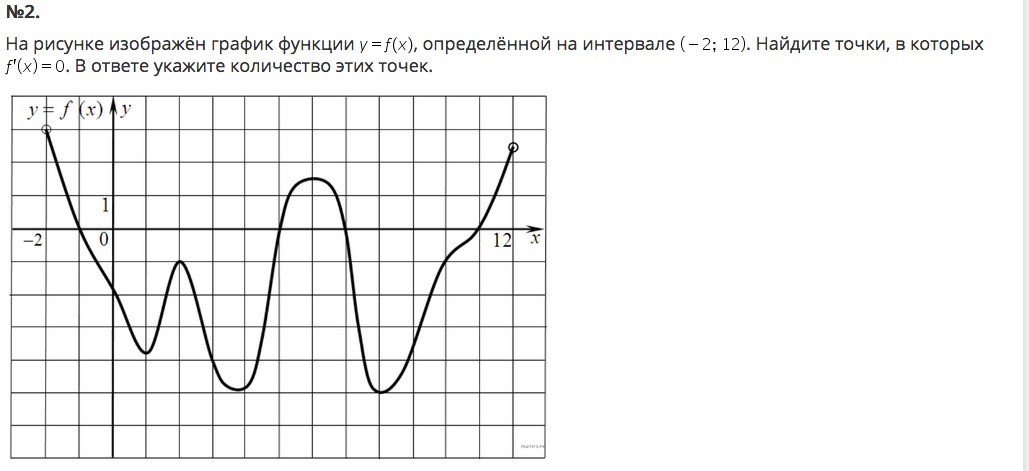потому как визуально, эти точки правее соседних слева минимумов)----------------------------#2 5 точек, смотреть рисунок
- Автор:
  finleykhan
- 6 лет назад
- 0
Добавить свой ответ