Задать вопрос Регистрация
Помочь другим

  • Помогите, пожалуйста, решить неравенство. Подробно.

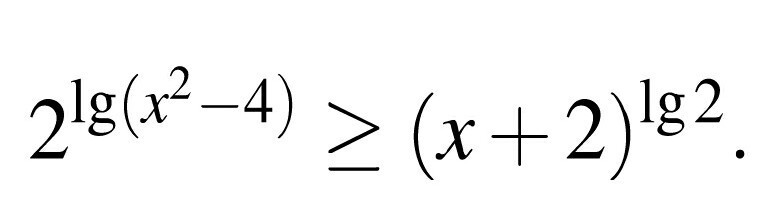
    question img

Ответы 6

  • изменил решение, написал подробнее
  • А почему (x^2-4)>0 перешёл в х-2>0?
  • это в силу того, что x+2>=0

    • Автор:

      heidi51
    • 6 лет назад
    • 0
  • вот если (x+3)*(x+5) > 0 и вместе с тем гарантированно, что x+4<0

    • Автор:

      odiefze7
    • 6 лет назад
    • 0
  • то (x+3)*(x+5) > 0 будет переходить в x+5 < 0
  • Возведение в степень на поле действительных чисел, когда и основание и степень и результат возведения действительны, не определено для отрицательного основания вообще. Другими словами, возводить отрицательные числа в не целые вещественные числа НЕЛЬЗЯ. Например, -3 в степень 1/3 нельзя возвести, вот извлечь корень кубический из -3 можно.по этому, нужно требовать, что бы x^2-4 \geq 0 (дальше в решении будет возникать, будет возводиться в вещественную степень lg(2)), и что бы x+2 \geq 0Также, нужно требовать, что бы x^2-4 eq 0, по скольку изначально x^2-4 находиться под логарифмом.Возведении отрицательных чисел в иррациональную степень происходит уже на поле комплекстных чисел, и будет получаться счётное число комплекстных значений такого возведения.Возведение отрицательных чисел в дробную степень, будет происходить также на поле комплекстных чисел, и будет получаться конечное число комплекстных значений такого возведения.lg(x^2-4)=log_{10}(x^2-4)=\frac{log_2(x^2-4)}{log_2(10)}=\frac{1}{log_2(10)}*log_2(x^2-4)=\\\\ =log_{10}(2)*log_2(x^2-4)=lg(2)*log_2(x^2-4)=\\\\=log_2[(x^2-4)^{lg(2)}],\ \ if\ \ x^2-4> 0------------------2^{lg(x^2-4)}=2^{log_2[(x^2-4)^{lg(2)}]}=(x^2-4)^{lg(2)},\ \ if\ \ x^2-4 > 0------------------2^{lg(x^2-4)}=2^{\frac{log_2(x^4-10)}{log_2(10)}}=2^{log_2(x^2-4)^{\frac{1}{log_2(10)}}}=\\\\ =(x^2-4)^{\frac{1}{log_2(10)}}=(x^2-4)^{lg(2)},\ \ if\ \ x^2-4 \ \textgreater \ 0------------------2^{lg(x^2-4)} \geq (x+2)^{lg(2)}\\\\ \left \{ {{(x^2-4)^{lg(2)} \geq (x+2)^{lg(2)}} \atop {x^2-4\ \textgreater \ 0}} ight. \\\\ \left \{ {{x^2-4} \geq x+2}} \atop {(x-2)(x+2)\ \textgreater \ 0\ \ and\ \ x+2 \geq 0}} ight. \\\\ \left \{ {{x^2-x-6} \geq 0}} \atop {x-2\ \textgreater \ 0}} ight. \\\\ \left \{ {{(x+2)(x-3)} \geq 0}} \atop {x\ \textgreater \ 2}} ight. \\\\ \left \{ {{x-3} \geq 0}} \atop {x\ \textgreater \ 2}} ight. \\\\ \left \{ {{x} \geq 3}} \atop {x\ \textgreater \ 2}} ight. \\\\ x \geq 3\\\\ x\in[3;\ +\infty)
    answer img

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years