-
как решать эти примеры? (интегралы) все на фото 18 и 19 задания
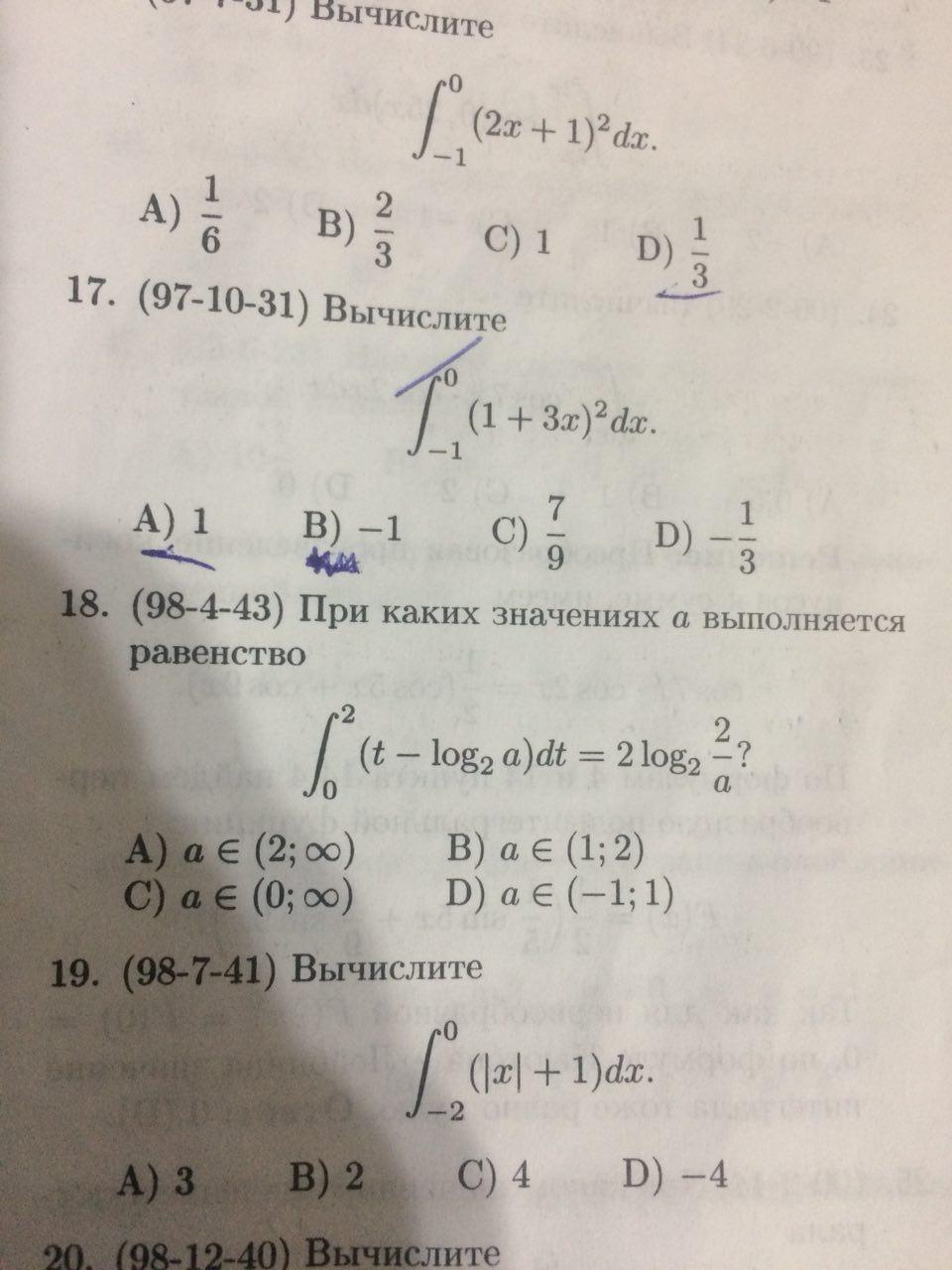
-
Предмет:
Алгебра -
Автор:
gingergt73 - 6 лет назад
-
Ответы 1
-
18. ОДЗ по логарифму а>0Вначале вычислить интеграл
t²/2 - t*log₂a |²₀ == (4/2 - 2log₂a) - (0 - 0) = 2 - 2log₂a = 2(1 - log₂a) == 2 (log₂2 - log₂a) = 2 log₂(2/a) ⇒
⇔
Полученное равенство справедливо для всех a>0 ⇒Ответ C) a∈(0; +∞)19. Так как функция f(x)=|x|+1 симметрична относительно прямой x=0 ⇒
⇔
x²/2 + x |²₀ = 2²/2 + 2 - 0 = 4Ответ С) 4Если решать без симметрии. Интервал интегрирования x∈[-2;0] ⇒-2 ≤ x ≤ 0 ⇒ |x| = -x
= x - x²/2 |⁰₋₂ = 0 - 0 - (-2 - (-2)²/2) = -(-4) = 4Ответ С) 4
-
Автор:
winniegndg - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
визначте об'єм вуглекислого газу ,що виділився при прожарюванні 1 кг технічного магній карбонату с масовою часткою домішок 16%
Срочно нужна помощь -
срочно решите срочно решите срочно решите срочно решите срочно решите
-
Предмет:
Информатика -
Автор:
janettavfao - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Самая большая микросхема компьютера
-
Предмет:
Информатика -
Автор:
siroqfk3 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- За кем была закреплина москва? Помогите срочно:(
How much to ban the user?
1 hour
1 day
100 years
