Решите уравнение . Через дискриминант , если это возможно

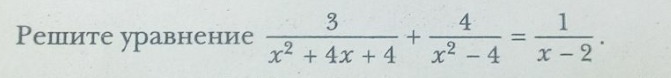
Ответы 1

При решении используем формулы сокращенного умножения:1) квадрат суммы(а + b)² = a² + 2ab +b²2) разность квадратова² - b² = (a - b)(a + b) $\frac{3}{x^2 +4x + 4} + \frac{4}{x^2 - 4} = \frac{1}{x - 2} \\ \\ \frac{3}{x^2 +2*x *2 + 2^2} + \frac{4}{x^2 - 2^2} = \frac{1}{x - 2} \\ \\ \frac{3}{(x+2)^2} + \frac{4}{(x-2)(x+2)} - \frac{1}{x - 2} = 0$ Знаменатели дробей не должны быть равны 0 ( на 0 делить нельзя), следовательно: х ≠ - 2 ; х ≠ 2Избавимся от знаменателей, умножим обе части уравнения на (x-2)(х+2)² :3(х - 2) + 4(х+2) - 1(х + 2)² = 0 *(х-2)(х+2)²3х - 6 + 4х + 8 - (х² + 4х + 4) = 0Перед скобкой знак "-" ⇒ меняем знаки выражения в скобках на противоположные :3х - 6 + 4х + 8 - х² - 4х - 4 = 0-х² + (3х + 4х - 4х) + (8 - 6 - 4) = 0 - х² + 3х - 2 = 0 | * (-1)x² - 3x + 2 = 0D = (-3)² - 4*1*2 = 9 - 8 = 1 = 1²D>0 - два корня уравненияx₁ = $\frac{- (-3) - 1}{2*1} = \frac{3 - 1}{2} = \frac{2}{2} = 1$ х₂ = $\frac{- (-3) + 1}{2*1} = \frac{3 + 1}{2} = \frac{4}{2} =2$ - не подходит ( т.к. х ≠ 2)Ответ : х = 1 .
- Автор:
  judith
- 5 лет назад
- 0
Добавить свой ответ