Задать вопрос Регистрация
Помочь другим

  • При каких значениях А сумма кубов корней уравнения будет максимальной?


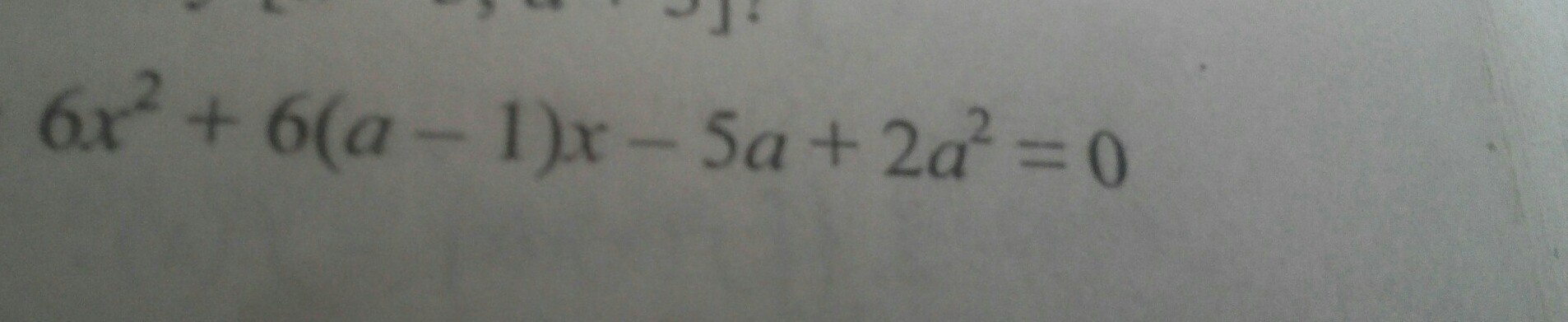
    question img

Ответы 1

  • 6x^2+6(a-1)x-5a+2a^2=0Разделим почленно уравнение на 6 чтобы получить приведенное уравнение:x^2+(a-1)x+ \dfrac{2a^2-5a}{6} =0Если это уравнение имеет корни, то их сумма равна второму коэффициенту, взятому с противоположным знаком:x_1+x_2=1-aа произведение корней равно свободному члену:x_1x_2=\dfrac{2a^2-5a}{6}Выразим сумму кубов через сумму и произведение. Возьмем сумму корней и возведем ее в куб:(x_1+x_2)^3=x_1^3+3x_1^2x_2+3x_1x_2^2+x_2^3Перегруппируем слагаемые в правой части:(x_1+x_2)^3=x_1^3+x_2^3+3x_1x_2(x_1+x_2)И выразим сумму кубов:x_1^3+x_2^3=(x_1+x_2)^3-3x_1x_2(x_1+x_2)Вычисляем сумму кубов:x_1^3+x_2^3=(1-a)^3-3\cdot\dfrac{2a^2-5a}{6}\cdot (1-a)= \\\ =1-3a+3a^2-a^3-(a^2-2.5a)(1-a)= \\\ =1-3a+3a^2-a^3-a^2+a^3+2.5a-2.5a^2= \\\ =-0.5a^2-0.5a+1Сумма кубов есть квадратичная функция от а с отрицательным старшим коэффициентом. Значит, ее максимум достигается в вершине при а, равном:a_m=- \dfrac{-0.5}{2\cdot(-0.5)} =- \dfrac{1}{2} =-0.5Убедимся, что при а=-0,5 исходное уравнение действительно имеет корни:6x^2-6\cdot(-0,5-1)\cdot x-5\cdot(-0.5)+2\cdot(-0.5)^2=0 \\\ 6x^2-9x+3=0 \\\ 2x^2-3x+1=0Сумма коэффициентов равна 0, корни уравнения 1 и 1/2.Ответ: при а=-0,5

    • Автор:

      finley34
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years