-
Задание 1.
Преобразуйте выражение, чтобы получить многочлен стандартного вида. Укажите степень многочлена.
Задание 2.
Докажите, что при любых целых значениях x многочлен делится на 7.
Задание 3.
Докажите, что при любых действительных значениях x многочлен не может принимать отрицательных значений.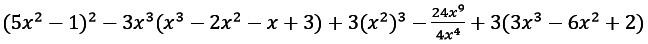
Ответы 5
-
вы с интернет урока?
-
Автор:
patcheshouse - 6 лет назад
-
0
-
-
в каком смысле?
-
Автор:
wolfgang - 6 лет назад
-
0
-
-
интернет урок - это что-то вроде спец. форума? Если вы о подобном, то нет; я обыкновенный ученик 9 класса
-
Автор:
calderon - 6 лет назад
-
0
-
-
нет, интернет урок это домашняя школа)
-
Автор:
emiliopearson - 6 лет назад
-
0
-
-
Многочлен стандартного вида:
4-я степень.Можно записать многочлен по-иному:
Очевидно, многочлен делится на 7, т.к. один из его множителей равен 7.Пусть,
Мы видим, что у нас только один возможный корень (значение нас не интересует), значит, график лишь 1 раз коснется оси X; значит минимальное значение многочлена - ноль, т.е. нет отрицательных значений
-
Автор:
bellbottoms - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Вычислить массу неоднородного тела, ограниченного поверхностями
z=x^2+y^2
z^2=x^2+y^2
y>=0
Функция плотности - р(x;y;z)=70yz -
у Олега 9 дисков с компьютерными играми на 5 дисках записана головоломки а на 6 квесты Сколько у Олега компьютерных дисков на которых записаны головоломки и квесты
-
Предмет:
Математика -
Автор:
bubblegumuklh - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Периметр прямоугольника 20 см.Найдите его площадь,если его ширина на 4 см короче длины.Начерти его полупериметр.
-
Предмет:
Математика -
Автор:
xzavieriwsk - 6 лет назад
-
Ответов:
7 -
Смотреть
-
-
За первый день консервный завод переработал 65 ящиков огурцов,а за второй 74 ящика.За второй день переработали на 1 ц 80кг больше огурцов ,чем за первый. Сколько килограммов огурцов переработал завод за-первый день?
можно пожалуйста с пояснениями-
Предмет:
Математика -
Автор:
emberztcw - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
