-
Решите 4-ое неравенство пожалуйста. Иди хотя-бы подскажите как решать.
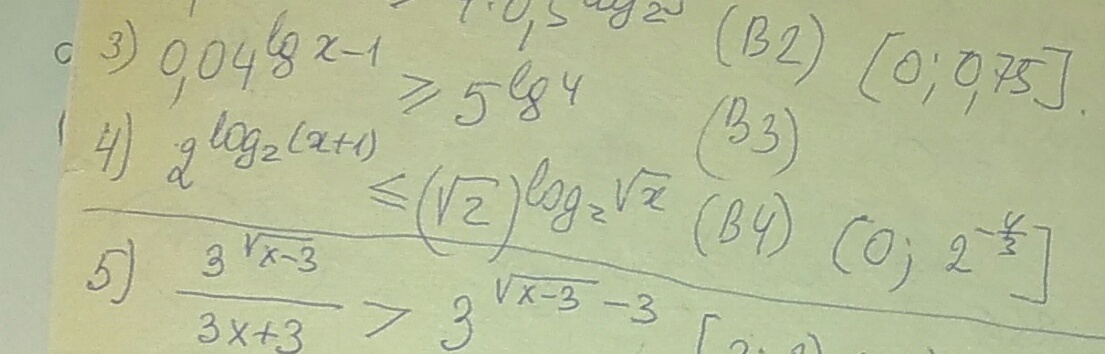
-
Предмет:
Алгебра -
Автор:
fun dipietq - 6 лет назад
-
Ответы 6
-
x=1 подходит, нигде нет ошибок, там решением будет одз
-
Автор:
kasen - 6 лет назад
-
0
-
-
Решение 1 не подходит. В правой части в степени будет 0. Получится 2<=1
-
Автор:
tyharvey - 6 лет назад
-
0
-
-
2 меньше либо равно 1*
-
Автор:
kalebbcv5 - 6 лет назад
-
0
-
-
Только что дополнительно проверил в вольфраме: решения действительно нет. Обратитесь к преподавателю. Например, смена знака неравенства в другую сторону помогла бы.
-
Автор:
gracelynwu - 6 лет назад
-
0
-
-
1. Для начала, надо сделать, чтобы основания в обоих частях неравенства были равны. Для этого в правой части заменяем корень из 2 на 2, НО при этом логарифм в степени в правой части неравенства умножаем на 1/2.2. Основания равны, а степень двойки является неубывающей функцией, значит обе части неравенства заменяем на то, что стоит в степенях двойки. Получаем: log2 (x+1) = 1/2 * log2 (sqrt(x)).3. Домножаем обе части на 2. Двойку в левой части неравенства переносим в степень подлогарифмической функции.4. Логарифм двойки есть функция неубывающая, значит производим замену аналогично п.2. Получим: (x+1)^2<=x^(1/2). Осталось решить обычное неравенство. Вот только проблема: это неравенство не имеет решения (проверьте сами). Возможно, в условии ошибка
-
Автор:
lili17e7 - 6 лет назад
-
0
-
-
2^log(2)(x+1)<=√(2)^(log(2)√(x)) 2^log(2)(x+1)<=2^(log(2)√(x)/2) 2log(2)(x+1)<=log(2)√(x) (x+1)^2<=√x x>0 (x+1)^4<=x Рассмотрим функцию f(x)=(x+1)^4-x f'(x)=4(x+1)^3-1 4(x+1)^3=1 x=(1/4)^(1/3)-1 Откуда при x=(1/4)^(1/3)-1 у функций минимум f((1/4)^(1/3)-1) = 0.52 Значит (x+1)^4-x>0 откуда (x+1)^4>x при любых x E (-oo;+oo) Значит решений нет
-
Автор:
teodora - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
найдите длину окружности, если длина её радиуса 2,25 дм.(Число π=3,14)
-
Предмет:
Математика -
Автор:
damian446 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
как решить пример 1,5+(-6)=?
-
Предмет:
Математика -
Автор:
general88 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Современниками были:
1. Иван Калита и Тохтамыш
2. Кузьма Минин и Иван Болотников
3.Иван Грозный и митрополит Алексей
4.Борис Годунов и Елена Глинская
Помогите пожалуйста очень срочно нужно.
дам 15 балов.-
Предмет:
История -
Автор:
adóntaylor - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Морфология
а) изучает особенности внутреннего строения организмов
б) описывает особенности внешнего строения организмов
в) выявляет особенности зародышевого развития организмов
г) изучает особенности строения тканей различных органов
д) особенности метаболизма
How much to ban the user?
1 hour
1 day
100 years
