Задать вопрос Регистрация
Помочь другим

  • Определить тип дифференциальных уравнения и найти его решения.

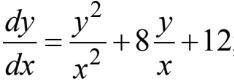
    question img

Ответы 6

  • В течении 2-х часов не будет кнопка изменить)

    • Автор:

      ashlee
    • 5 лет назад
    • 0
  • у вас есть 2 часа до того как добавили ответ
  • т.е. через 2 часа не могу менять уже ? понял - спасибо

    • Автор:

      dandyydix
    • 5 лет назад
    • 0
  • Да)
  • Если есть время посмотри вопрос https://znanija.com/task/29248368 типа моего постоянного клиента =) заранее спасибо.

    • Автор:

      diesel
    • 5 лет назад
    • 0
  • Тип: дифференциальное уравнение первого порядка разрешенной относительно производной, однородное.Пусть y=ux, тогда y'=u'x+u получимu'x+u= \dfrac{u^2x^2}{x^2}+8\cdot \dfrac{ux}{x} +12\\ \\ u'x+u=u^2+8u+12\\ \\ u'x=u^2+7u+12Получили уравнение с разделяющимися переменными, разделяя переменные имеем\displaystyle \int \frac{du}{u^2+7u+12}=\int \frac{dx}{x} ;~~~\Rightarrow~~~ \int\bigg( \frac{1}{u+3}- \frac{1}{u+4}\bigg)du=\int \frac{dx}{x} \ln|u+3|-\ln|u+4|=\ln|x|+\ln C\\ \\ \ln \bigg |\dfrac{u+3}{u+4}\bigg| =\ln |xC|\\ \\ \\ Cx=1-\dfrac{1}{u+4}~~\Rightarrow~~~ u+4= \dfrac{1}{1-Cx} ~~\Rightarrow~~ u= \dfrac{4Cx-3}{1-Cx} Возвращаемся к обратной замене \dfrac{y}{x} =\dfrac{4Cx-3}{1-Cx}~~~\Rightarrow~~~ \boxed{\dfrac{4Cx^2-3x}{1-Cx}} - общее решение

    • Автор:

      sundance
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years