-
ПОМОГИТЕ ПОЖАЛУЙСТА!!! ОЧЕНЬ ВАЖНО!!! 15 ЗАДАНИЕ ЕГЭ!!
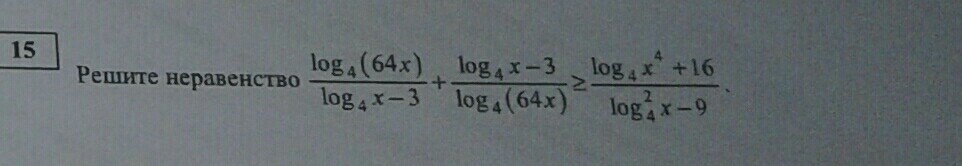
-
Предмет:
Алгебра -
Автор:
ascensióneu3j - 6 лет назад
-
Ответы 5
-
спасибо большое❤
-
Автор:
brysonfernandez - 6 лет назад
-
0
-
-
извиняюсь очень - нашел у себя в решении, почти в конце, ошибку. модераторы, прошу дать исправить ))
-
Автор:
calvin - 6 лет назад
-
0
-
-
В ответе у уже написанному надо приписать х = 4, т.к. при t=1 неравенство также верно.
-
Автор:
cannoli - 6 лет назад
-
0
-
-
ничего, бывает
-
Автор:
jackson58 - 6 лет назад
-
0
-
-
ОДЗ: x>0
+ - - + ----o------|------o-----> t -3 1 3t < -3 или t > 3 или t = 1
или
или
С учетом ОДЗ:
Ответ:
-
Автор:
almudenawalker - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- y=x^5+5x^4+5x^3+1,[-2;1]
-
90÷5 разным способом
-
Предмет:
Математика -
Автор:
kendalldhte - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
finish the idiom: "walking on the ...
-
Предмет:
Английский язык -
Автор:
bradleycarroll - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
известный русский поэт 20в рассматривал свои произведения как целостный роман в стихах
-
Предмет:
Литература -
Автор:
currydelgado - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
