-
найдите 5S,если
S=1/6 + 2/6^2 + 3/6^3 + ... + n/6^n+...
Пожалуйста очень надо))
это относиться к теме "числовая последовательность;Прогрессия"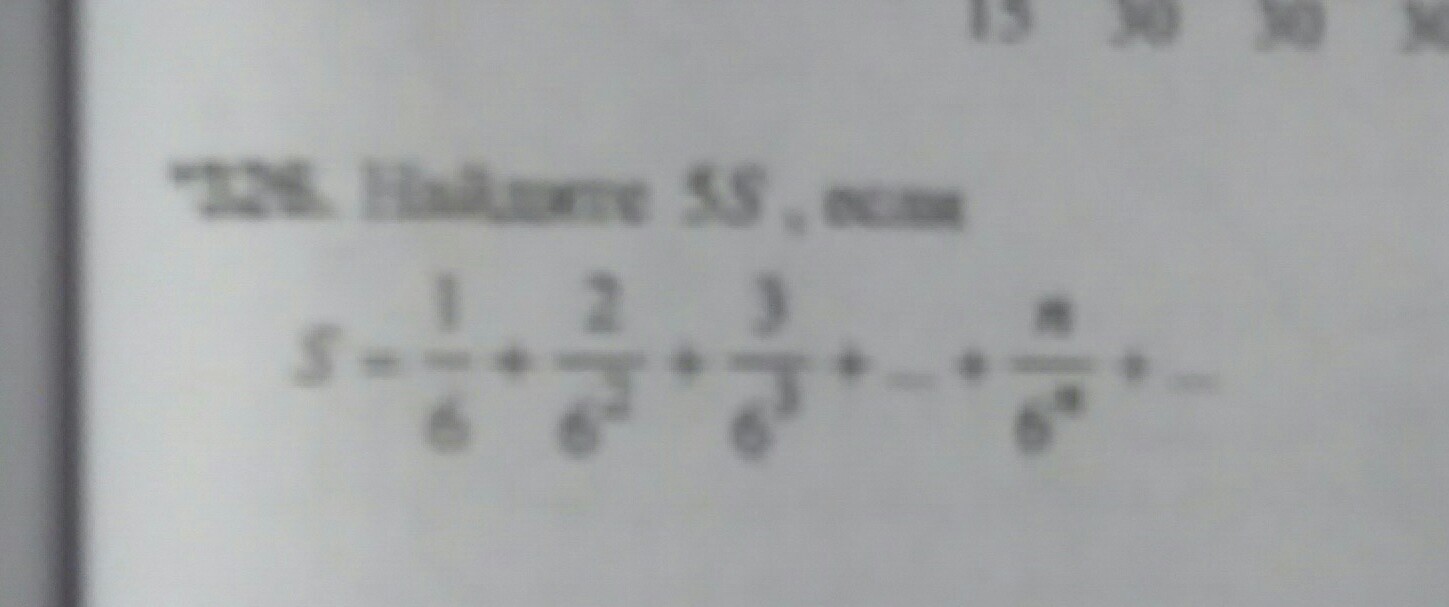
-
Предмет:
Алгебра -
Автор:
ireneoxmxq - 6 лет назад
-
Ответы 2
-
спасибо большое
-
Автор:
flintramsey - 6 лет назад
-
0
-
-
Разделяя не слагаемые S1=(1/6+1/6^2+1/6^3+...+1/6^n) S2=(1/6^2+1/6^3+...+1/6^n) S3=(1/6^3+1/6^4+...+1/6^n) .... значит Для S1 получаем бесконечно убывающую геометрическую прогрессию, откуда S1=(1/6)/(1-1/6)=1/5 ДляS2=S1-1/6 Для S3=S1-(1/6+1/6^2) Для S4=S1-(1/6+1/6^2+1/6^3) И т д По формуле геометрической прогрессии 1/6+1/6^2=(1/6)(1-(1/6)^2)/(5/6)=1/5*(1-1/6^2) Значит S3=1/5(1-1+1/6^2)=1/5*(1/6)^2 S4=1/5*(1/6)^3 И т д Значит вся сумма Есть S=1/5+1/5*(1/6+1/6^2+...+1/6^n)= 1/5*(1+1/6+1/6^2+...+1/6^n) Так как нужно найти 5S , то 5S=1+1/6+...+1/6^n Бесконечно убывающая прогрессия 5S=1/(1-(1/6))=6/5
-
Автор:
villa - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Какие члены предложения называются однородными??
-
Предмет:
Русский язык -
Автор:
trouble - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Наибольшее из 4 чисел,каждое из которых меньше предыдущего на 19 единиц,равна 135.Чему равна сумма этих чисел. Умололяяяяяяяяяяяяяюююююююююю.
-
Предмет:
Математика -
Автор:
dorkxpud - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Хэлп
(x+5)(x-8)<0
(x+2)(x+1/2)<0
Решить методом интервалов-
Предмет:
Алгебра -
Автор:
ice queenqb9h - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите пожалуйста Массасы 300 кг сүтті қыздырғанда 60 кДж жылу мөлшері бөлінді.Бұл процестегі температураның өзгерісін анықта(сүттің меншікті жылу сыйымдылығы с=3940 Дж/кг*С)
-
Предмет:
Физика -
Автор:
gunthertate - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
