-
решить неравенство
очень нужно решение,был сегодня егэ,сомневаюсь в своем ответе,но очень хочется узнать правильно или нет решено)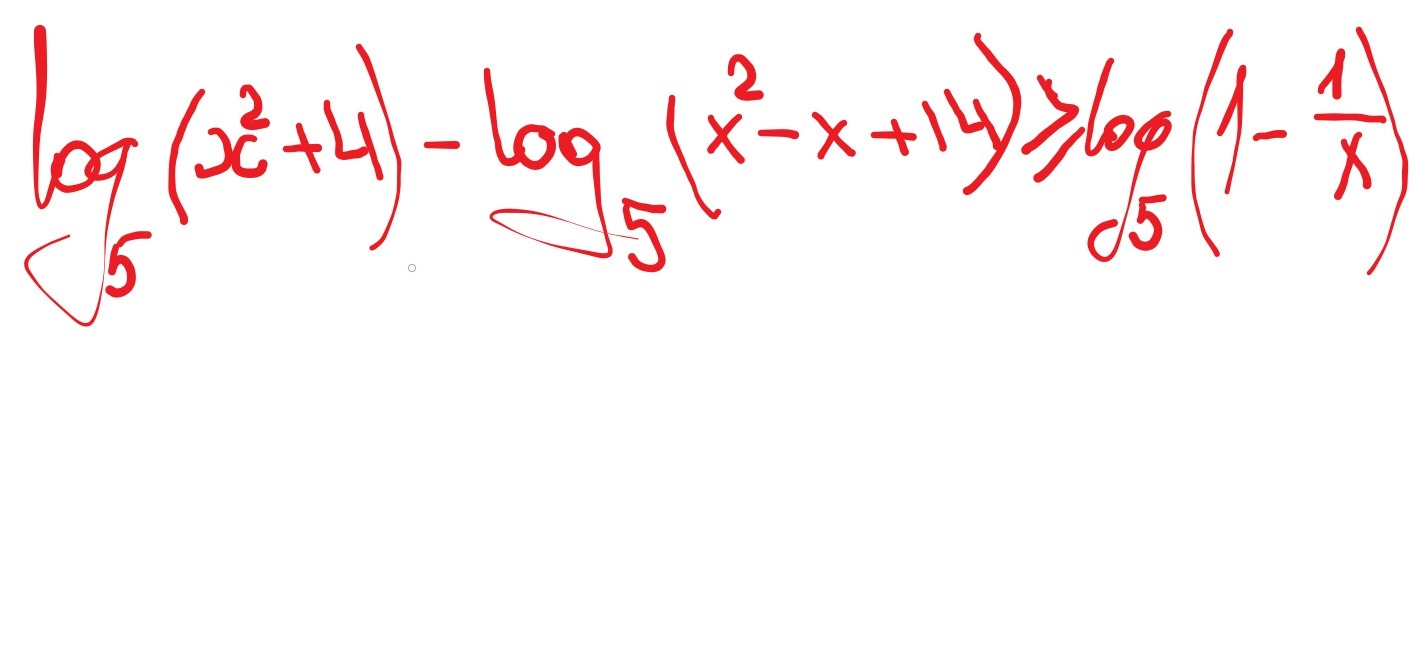
Ответы 4
-
Здравствуйте! Очень прошу помочь Мат. ожидание стратегия игрыhttps://znanija.com/task/29274828 - 50+25 балов
-
Автор:
holt - 6 лет назад
-
0
-
-
Здравствуйте! Очень прошу помочь Мат. ожидание стратегия игрыhttps://znanija.com/task/29274828 - 50+25 балов
-
Автор:
bootsiepinw - 6 лет назад
-
0
-
-
log(5) (x²+4) - log(5) (x²-x+14) ≥ log(5) (1 - 1/x) надо сразу находить ОДЗпервый - вся числовая ось всегда положителенвторой D=1-4*14<0 и коэффициент при квадрате больше 0 - тоже всегда положителен1-1/x>0(x-1)/x>0++++++++(0) ------------- (1) ++++++++x∈(-∞ 0) U (1 +∞) по правилу вычитания логарифмовlog(5) (x²+4) / (x²-x+14) ≥ log(5) (1 - 1/x)снимаем логарифмы - знак оставляем (основание больше 1)(x²+4) / (x²-x+14) ≥ (x - 1)/x (x²+4) / (x²-x+14) - (x - 1)/x ≥ 0к общему знаменателю ( (x²+4)*x -(x-1) (x²-x+14) ) /( x(x²-x+14) ) ≥ 0 теперь в знаменателе x²-x+14 можно отбросить как всегда положительнрое ( x³+4x -(x³-x²+14x-x²+x-14)) / x ≥ 0 ( x³+4x -(x³-2x²+15x-14)) / x ≥ 0 ( x³+4x -x³+2x²-15x+14)) / x ≥ 0 ( 2x²-11x+14)) / x ≥ 0D=121-4*2*14=121-112=3²x12=(11+-3)/4 = 2 7/22(x-2)(x-7/2) / x ≥ 0опять метод интервалов---------- (0) ++++++ [2] ---------- [7/2] +++++++++пересекаем с ОДЗ x∈(-∞ 0) U (1 + ∞)Ответ (1 2] U [7/2 +∞)
-
Автор:
giovannahyqh - 6 лет назад
-
0
-
-
--------------------------------

-
Автор:
muscles - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
(2корень из 3)^2/12 помогитеее
-
Предмет:
Математика -
Автор:
shayna - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Write an account of your best/worst holiday.
Write about: who you went with
where you went and what you did
what made the holiday so special unpleasant your feelings-
Предмет:
Английский язык -
Автор:
jamaril1w5 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Помогите ответить на вопросы по английскому!! Полный ответ на английском
-
Предмет:
Английский язык -
Автор:
rodrigozyfe - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- какие из пар чисел (2;2) (-3;4;) (8;0) является решением уравнения 5у-2х=26(распишите)
How much to ban the user?
1 hour
1 day
100 years
