-
Добрый день! Пожалуйста, скиньте решение с объяснением. Заранее спасибо!
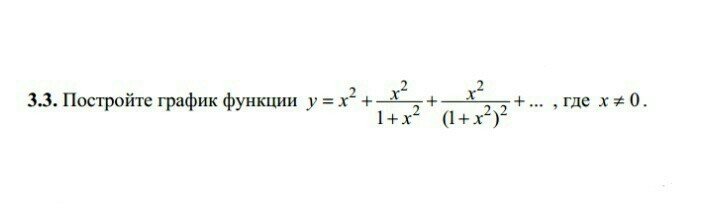
-
Предмет:
Алгебра -
Автор:
esiquiofox - 6 лет назад
-
Ответы 1
-
Это геометрическая убывающая последовательность с первым членом
и знаменателем
специально отметим, что при ограничении
cумма бессконечной убывающей прогрессии:
графиком функции оказалась парабола с вершиной в точке
, которая ВЫКОЛОТАпарабола симетрична относительно оси ОХи может быть построена по точкам:(1; 2), (2; 5), (3; 10)(-1; 2), (-2; 5), (-3; 10)
-
Автор:
braylonqy5f - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в
километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по
графику, на какой высоте атмосферное давление равно 320 миллиметрам ртутного столба.
Ответ дайте в километрах-
Предмет:
Алгебра -
Автор:
adalynntapia - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- помогите пожалуйста!!! найдите площадь фигуры,ограниченной параболой у=(х+1)^2 ,прямой у=1-х и осью ох
- За 6 кг апельсинів і 3 кг бананів заплатили 39 грн, а 9 кг апельсинів дорожчі за 5 кг бананів на 30 грн.Скільки коштує 1 кг апельсинів і скільки коштує 1 кг бананів?
-
выберите 3 правильных ответа: а)развитие второго круга кровообращения связано с выходом позвоночного на сушу б)сквозная пищеварительная система впервые появилась у плоских червей в)все личики земноводных дышат лёгкими и кожей г)кора головного мозга впервые появилась у млекопитающих д)четырехкамерное сердце обеспечило разделение крови на венозную и артериальную е)теплокровные животные шире распространены на Земле ,чем хладнокровные
-
Предмет:
Биология -
Автор:
amarisferrell - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
