-
СРОЧНО!!!
Пожалуйста, решите 9 и 10, заранее спасибо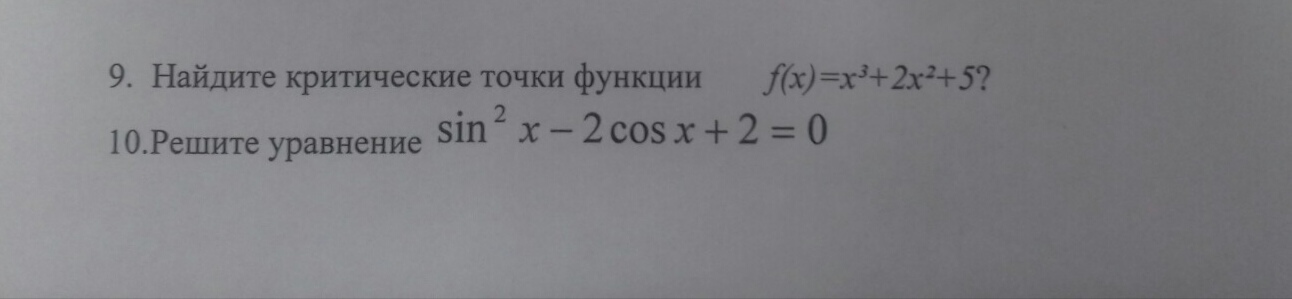
-
Предмет:
Алгебра -
Автор:
stephengrant - 6 лет назад
-
Ответы 5
-
Ща буду редактировать, я кучу корней упустил.
-
Автор:
rush - 6 лет назад
-
0
-
-
Редактировал! Просто забыл, что у тригонометрических уравнений куча корней.
-
Автор:
martínezodyo - 6 лет назад
-
0
-
-
Спасибо Вам большое)
-
Автор:
apollo - 6 лет назад
-
0
-
-
10)(sinx)^2 - 2*cosx + 2 = 0;Применяем формулу: (sinx)^2 = 1 - (cosx)^2;1 - (cosx)^2 - 2*cosx + 2 = 0;(cosx)^2 + 2 * cosx - 3 = 0;Заменяем: cosx = t;t^2 + 2 * t - 3 = 0;Я не хочу использовать формулу корней квадратного уравнения, поэтому я разложу на множители:t^2 + 3*t - t - 3 = 0;t*(t+3)-(t+3) = 0;(t+3)*(t-1) = 0;Мы видим тут два корня: t = 1 и t = -3;Возвращаемся к замене: t = cosx;То есть: cosx = 1 и cosx=-3;В первом случае: cosx = 1, то есть x = 2*(pi)*k, где k Є Z.Во втором случае корня нет, так как косинус не может быть равен -3: Итак, ответ: x = 2*(pi)*k, где k Є Z.9) Как я понял надо найти значения икса, при которых производная равна нулю.(x^3 + 2*x^2 + 5)' = 3*x^2 + 4*x;3*x^2 + 4*x = 0;x*(3*x + 4) = 0;x = 0 и x = -4/3;С девятой задачей я схалтурил, но десятую точно решил правильно!
-
Автор:
emery - 6 лет назад
-
0
-
-
9)f(x)=x³+2x²+5f'(x)=3x²+4xf'(x)=03x²+4x=0;x(3x+4)=0x=0;3x+4=0;x=-4/310)sin²x-2cosx+2=01-cos²x-2cosx+2=0cosx=tt²+2t-3=0D=4+12=16=4²t=(-2±4)/2t1=-3t2=1cosx=-3; нет решенияcosx=1x=2πk;k€Z
-
Автор:
lovelysftm - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Який об'єм рідкого шлікеру насос з ккд 50% що споживає 24 Вт,піднімає на висоту 12 м за 30 хв густина шлікеру 1.4*10^-3кг/м
-
Решить логарифмическое уравнение lg(x^2-9)=lg(4x+3)
-
Предмет:
Математика -
Автор:
tyronerich - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Цену на некоторый товар сначала снизили на 30%, а затем повысили на 20%.
На сколько процентов изменилась первоначальная цена товара?-
Предмет:
Алгебра -
Автор:
adelinekzfk - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Помогите,пожалуйста решить уравнения.
3−sin(2х−/6)= 12
2cos(2−3х)=1
How much to ban the user?
1 hour
1 day
100 years
