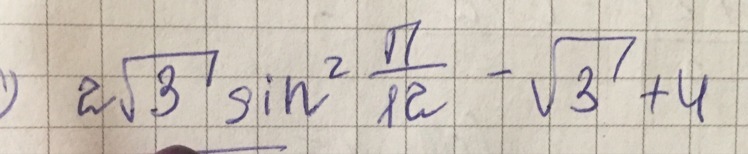Ответы 2
-
1 - 2sin²x = cos2xОтвет: 2,5
-
Автор:
doriansnwz - 6 лет назад
-
0
-
-
Используя формулу
,записать выражение в развёрнутом виде:
;
Вычислить выражение,используя таблицу значений тригонометрических функций(можно найти в Интернете) и сократить на 2:
;
Распределить √3 через скобки:
;
Сократить противоположные выражения:
;
Вычислить сумму:
-
Автор:
eli - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Помогите с цепочкой
HCl-X1-KClO3-X2-HCl-X3-Cl2 -
Всем привет. Задача на фотке. Площадь криволинейной трапеции
-
Предмет:
Математика -
Автор:
mcgrath - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
0.9 делённое на 1 + 1 делённое на 8
-
Предмет:
Алгебра -
Автор:
harpostrickland - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
знайдіть область визначення функції у=√18-9х-2х(у квадраті)
-
Предмет:
Геометрия -
Автор:
diegogomez - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years