Для каждого значения а решить уравнение

Для каждого значения а решить уравнение
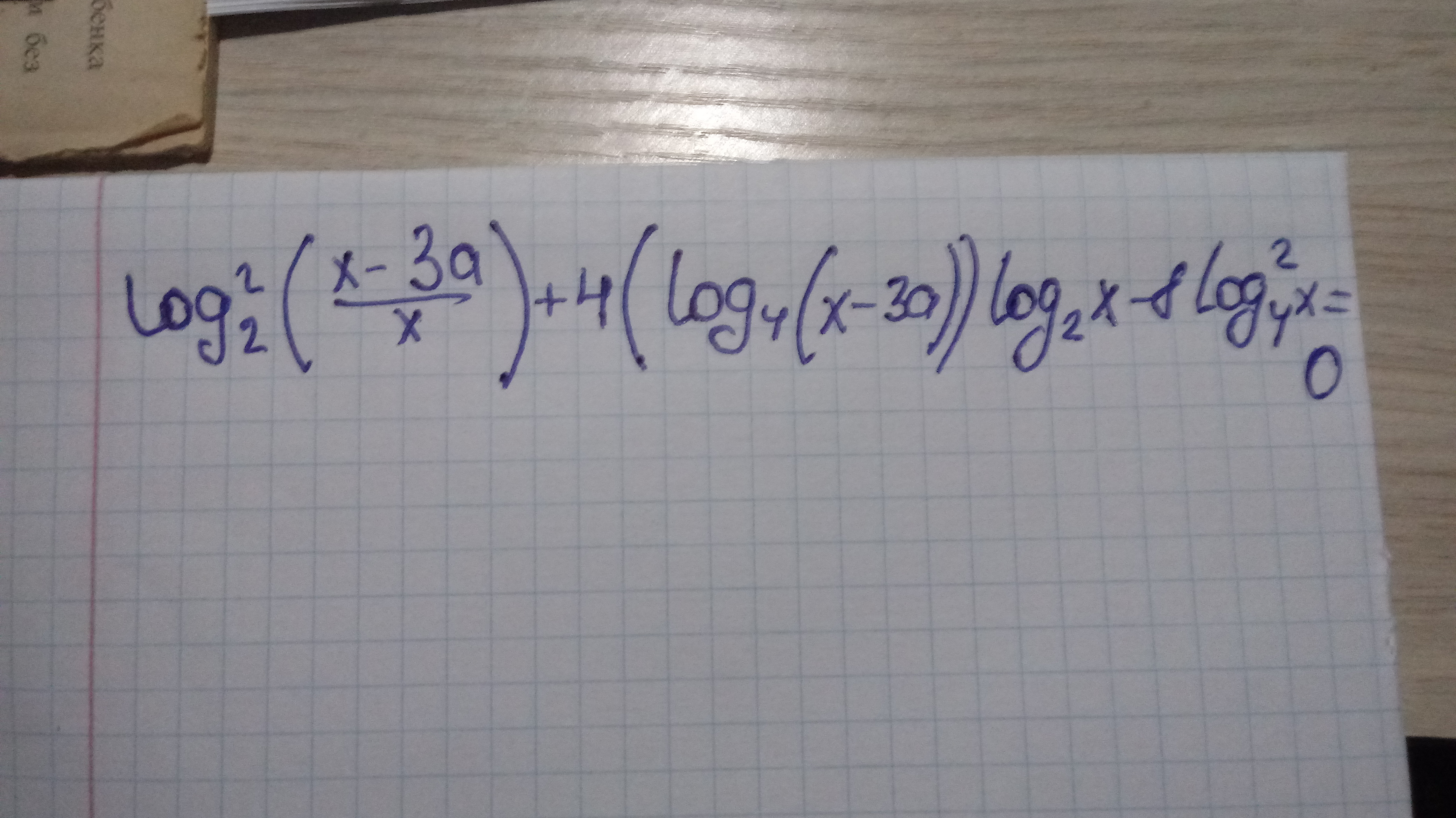
- Предмет:
  Алгебра
- Автор:
  jayvonrollins
- 6 лет назад

Ответы 4

Так какие значения а получаются? 1)0 и 2)все кроме 0
- Автор:
  layla68
- 6 лет назад
- 0
У тебя ошибка... Там же 8log^2 х по основанию 4... А значит получится 4log^2 х по основанию 2
- Автор:
  leonbrock
- 6 лет назад
- 0
Там в квадрате. log(4, x) = 1/2 log(2, x), значит, log(4, x)^2 = 1/4 log(2, x)^2
- Автор:
  joker6urp
- 6 лет назад
- 0
ОДЗ: x > 0, x - 3a > 0.
$\log_2^2\left(\dfrac{x-3a}xight)+4\log_4(x-3a)\log_2x-8\log_4^2x=0$
Приводим все логарифмы к одинаковому основанию по формуле $\log_{a^k}b=\frac1k\log_ab$ :
$\log_2^2\left(\dfrac{x-3a}xight)+2\log_2(x-3a)\log_2x-2\log_2^2x=0$
Переписываем логарифм частного как разность логарифмов и раскрываем квадрат разности:
$\left(\log_2(x-3a)-\log_2xight)^2+2\log_2(x-3a)\log_2x-2\log_2^2x=0\\(\log_2^2(x-3a)-2\log_2(x-3a)\log_2x+\log_2^2x)+\\+2\log_2(x-3a)\log_2x-2\log_2^2x=0\\\log_2^2(x-3a)-\log_2^2x=0$
Получили разность квадратов. Раскладываем на множители:
$(\log_2(x-3a)-\log_2x)(\log_2(x-3a)+\log_2x)=0$
Произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит, уравнение выше на ОДЗ эквивалентно совокупности двух уравнений:
$\left[\begin{array}{l}\log_2(x-3a)-\log_2x=0\\\log_2(x-3a)+\log_2x=0\end{array}ight.\quad\left[\begin{array}{l}\log_2(x-3a)=\log_2x\\\log_2(x-3a)=\log_2\dfrac1x\end{array}ight.\\\left[\begin{array}{l}x-3a=x\\x-3a=\dfrac1x\end{array}ight.$
Перед тем, как идти дальше, хочется отметить, что если x > 0, то из равенств выше автоматически x - 3a > 0. Значит, при отборе корней можно будет проверить только неравенство x > 0, второе неравенство из ОДЗ будет выполнено, если выполнено первое.
Решаем дальше:
– первое уравнение совокупности:
x - 3a = x
3a = 0
a = 0
Если a = 0, то решение – x ∈ R (с учетом ограничений ОДЗ x > 0)
– второе уравнение совокупности:
$x-3a=\dfrac1x\\x(x-3a)=1\\((x-1.5a)+1.5a)((x-1.5a)-1.5a)=1\\(x-1.5a)^2-2.25a^2=1\\(x-1.5a)^2=2.25a^2+1>0\\x-1.5a=\pm\sqrt{2.25a^2+1}\\x=1.5a\pm\sqrt{2.25a^2+1}$
Нужно проверить, при каких a найденное решение удовлетворяет ОДЗ.
1) $x=1.5a+\sqrt{2.25a^2+1}>0$
$\sqrt{2.25a^2+1}>-1.5a$
Если a > 0, неравенство выполняется: левая часть положительна, правая отрицательная.
Пусть a < 0, тогда обе части неравенства положительны, можно возвести в квадрат
$2.25a^2+1>2.25a^2\\1>0$
Это неравенство выполнено также при всех a.
2) $x=1.5a-\sqrt{2.25a^2+1}$
Аналогично первому корню, можно проверить, что этот корень отрицательный при всех a, и поэтому не удовлетворяет ОДЗ.
Ответ: все x > 0 при a = 0, $x=1.5a+\sqrt{2.25a^2+1}$ при a ≠ 0.
- Автор:
  daffyrios
- 6 лет назад
- 0
Добавить свой ответ