Задать вопрос Регистрация
Помочь другим

  • Есть ответ задания , но я не могу к нему дойти ,понять алгоритм действий помогите по этапно сделать и в 2 способа через корни или вычисление с дробью

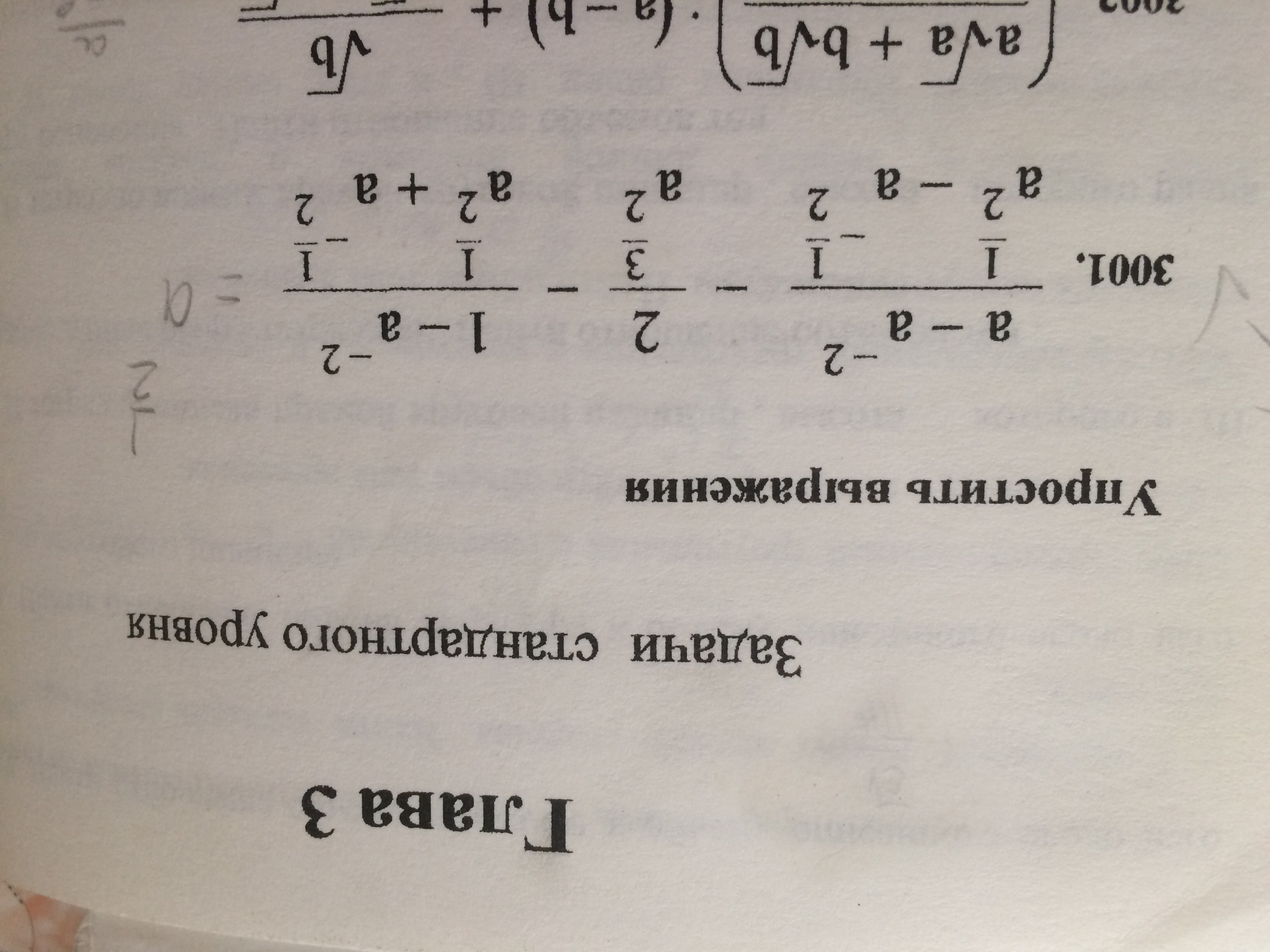
    question img

Ответы 1

  • 1-й способ:

    \dfrac{a^{-2}(a^3-1)}{a^{-\frac{1}{2}} (a-1)}-\dfrac{2}{a^{\frac{2}{3}}} -\dfrac{a^{-2}(a^2-1)}{a^{-\frac{1}{2}} (a+1)}=\\ =\dfrac{(a-1)(a^2+a+1)}{a^{\frac{3}{2}}(a-1)}-\dfrac{2}{a^{\frac{2}{3}}} -\dfrac{(a-1)(a+1)}{a^{\frac{3}{2}} (a+1)}=\\ =\dfrac{a^2+a+1}{a^{\frac{3}{2}}}-\dfrac{2}{a^{\frac{2}{3}}} -\dfrac{a-1}{a^{\frac{3}{2}} }=\\ =\dfrac{a^2+a+1-2-a+1}{a^{\frac{3}{2}}}= \dfrac{a^2}{a^{\frac{3}{2}}} = a^{\frac{1}{2}}

    2-й способ:

    \dfrac{a- \frac{1}{a^2} }{ \sqrt a - \frac{1}{\sqrt a} }- \dfrac{2}{a \sqrt a} - \dfrac{1- \frac{1}{a^2} }{ \sqrt a + \frac{1}{\sqrt a} }=\dfrac{ \frac{a^3-1}{a^2} }{\frac{a-1}{\sqrt a} } - \dfrac{2}{a \sqrt a} - \dfrac{ \frac{a^2-1}{a^2} }{\frac{a+1}{\sqrt a} } = \\ = \dfrac{(a-1)(a^2+a+1)\sqrt a}{a^2(a-1)} - \dfrac{2}{a \sqrt a} - \dfrac{(a-1)(a+1)\sqrt a}{a^2(a+1)}=

    = \dfrac{a^2+a+1}{a \sqrt a} -\dfrac{2}{a \sqrt a} - \dfrac{a-1}{a \sqrt a} = \dfrac{a^2+a+1-2-a+1}{a \sqrt a} =\dfrac{a^2}{a \sqrt a} =\\ =\dfrac{a}{ \sqrt a} =\sqrt a .

    answer img

    • Автор:

      rylan284
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years