Задать вопрос Регистрация
Помочь другим

  • Помогите пожалуйста!!! Очень срочно!!! Решить по действиях, примеры 4 и 36

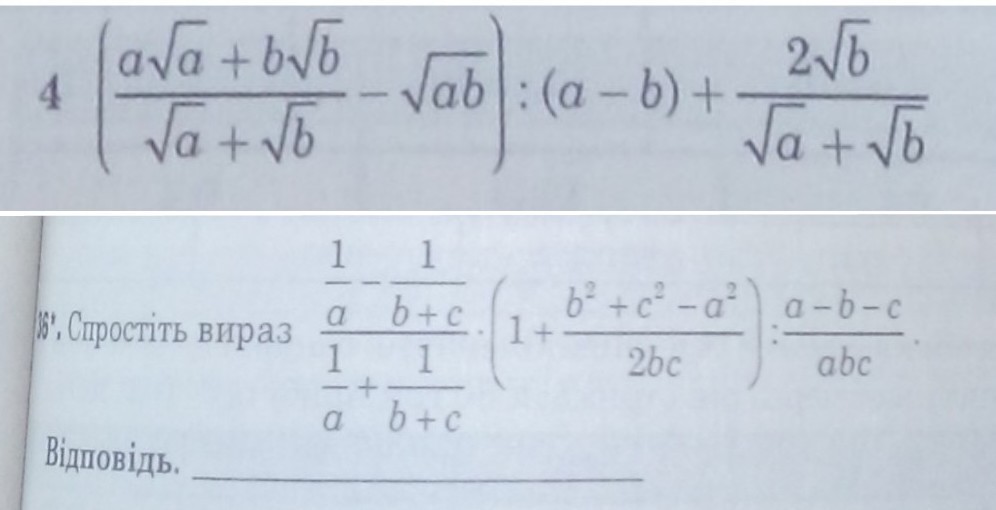
    question img

Ответы 4

  • В 5 пункте №36 не дописали (a+b+c) в знаменатель

    • Автор:

      poole
    • 6 лет назад
    • 0
  • Спасибо! Увидел, исправил, правда, грязновато получилось

  • 4)\; \; (\frac{a\sqrt{a}+b\sqrt{b}}{\sqrt{a}+\sqrt{b}}-\sqrt{ab}):(a-b)+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}=\\\\=(\frac{(\sqrt{a}+\sqrt{b})(a-\sqrt{ab}+b)}{\sqrt{a}+\sqrt{b}}-\sqrt{ab})\cdot \frac{1}{(a-b}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}=\\\\=\frac{a-2\sqrt{ab}+b)}{(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}=\frac{(\sqrt{a}-\sqrt{b})^2}{(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}=\\\\=\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}=\frac{\sqrt{a}-\sqrt{b}+2\sqrt{b}}{\sqrt{a}+\sqrt{b}}=\frac{\sqrt{a}+\sqrt{b}}{\sqrt{a}+\sqrt{b}}=1

    36)\; \; \frac{\frac{1}{a}-\frac{1}{b+c}}{\frac{1}{a}+\frac{1}{b+c}}\cdot (1+\frac{b^2+c^2-a^2}{2bc}}):\frac{a-b-c}{abc}=\\\\=\frac{b+c-a}{b+c+a}\cdot \frac{(2bc+b^2+c^2)-a^2}{2bc}\cdot \frac{abc}{a-b-c}=\\\\=\frac{-(a-b-c)}{a+b+c}\cdot \frac{(b+c)^2-a^2}{2bc}\cdot \frac{abc}{a-b-c}=\frac{-1}{a+b+c}\cdot \frac{(b+c-a)(b+c+a)}{2bc}\cdot \frac{abc}{1}=\\\\=\frac{-1\cdot (b+c-a)\cdot a}{2}=\frac{a\cdot (a-b-c)}{2}

    • Автор:

      heidy
    • 6 лет назад
    • 0

  • !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

    answer img

    • Автор:

      erinq1yl
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years