Здравствуйте, объясните, пожалуйста, как решаются подобные уравнения?

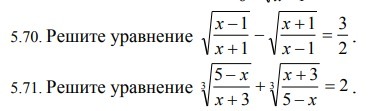
Ответы 4

во 2 примере должно 1 получиться, судя по ответам... Или в ответах опечатка
- Автор:
  floyd92
- 6 лет назад
- 0
Да, получится 1, у меня была описка.
- Автор:
  estherbrewer
- 6 лет назад
- 0
Спасибо за поправку
- Автор:
  weiss
- 6 лет назад
- 0
$1)\; \; \sqrt{\frac{x-1}{x+1}}-\sqrt{\frac{x+1}{x-1}}=\frac{3}{2}\; ,\\\\ODZ:\; \; \left \{ {{\frac{x-1}{x+1}\geq 0} \atop {\frac{x+1}{x-1}\geq 0}} ight. \; \; \Rightarrow \; \; x\in (-\infty ,-1)\cup (1,+\infty )\\\\t=\sqrt{\frac{x-1}{x+1}}\geq 0\; ,\; \; t-\frac{1}{t}=\frac{3}{2} \; ,\; \; \frac{2t^2-3t-2}{2t}=0\; ,\\\\2t^2-3t-2=0\; ,\; D=25\; ,\; \; t_1=2\; ,\; \; t_2=-\frac{1}{2}<0\\\\\sqrt{\frac{x-1}{x+1}}=2\; ,\; \; \frac{x-1}{x+1}=4\; ,\; \; x-1=4x+4\; ,\; \; 3x=-5\; ,\; x=-\frac{5}{3}\\\\Otvet:\; \; x=-1\frac{2}{3}.$
$2)\; \; \sqrt[3]{\frac{5-x}{x+3}}+\sqrt[3]{\frac{x+3}{5-x}}=2\\\\t=\sqrt[3]{\frac{5-x}{x+3}}\; , \; \; t+\frac{1}{t}=2\; ,\; \; \frac{t^2-2t+1}{t}=0\; ,\; \; (t-1)^2=0\; ,\; t=1\; ,\\\\\sqrt[3]{\frac{5-x}{x+3}}=1\; \; \Rightarrow \; \; \frac{5-x}{x+3}=1\; ,\; \; \frac{5-x}{x+3}-1=0\\\\\frac{2-2x}{x+3}=0\\\\2-2x=0\; \; \Rightarrow \; \; x=1\\\\Otvet:\; \; x=1.$
- Автор:
  jensenkey
- 6 лет назад
- 0
Добавить свой ответ