помогите пожалуйста, тригонометрическое уравнение, СРОЧНО помогите!!!!!

помогите пожалуйста, тригонометрическое уравнение, СРОЧНО помогите!!!!!
- Предмет:
  Алгебра
- Автор:
  freckles
- 6 лет назад

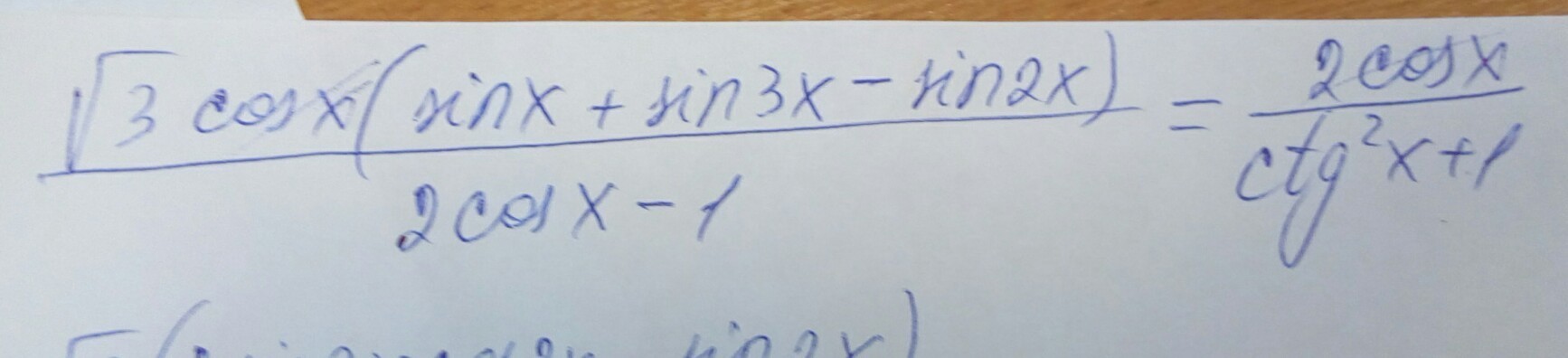
Ответы 7

ну у меня в принципе то же вышло, спасибо за подробное решение
- Автор:
  duchess
- 6 лет назад
- 0
верно , спасибо.
- Автор:
  venancio
- 6 лет назад
- 0
Ответ: π/2 +πn ; - 2π/3 +2πn
- Автор:
  junei8dy
- 6 лет назад
- 0
4π/3 + 2πn =2π -2π/3 +2πn= - 2π/3 +2π(n+1) = - 2π/3 +2πk
- Автор:
  morganhurst
- 6 лет назад
- 0
опечатку я видел, строкой выше всё верно, не так ли? ну, поэтому жду спокойно работу модератора )))
- Автор:
  elliotmann
- 6 лет назад
- 0
Вижу так. ..
О.Д.З.: $\cos x eq \frac{1}{2} ;\ \sin x eq 0$
$xeq \б \frac{\pi}{3} +2\pi k;\ xeq \pi k;\ k \in Z.$
Преобразуем уравнение:
$\sqrt{3} \cos x (\sin x+ \sin3x -\sin 2x)=2\cos x \sin^2x(2\cos x-1)\\ \sqrt{3} \cos x (2\sin 2x \cos x -\sin 2x)=2\cos x \sin^2x(2\cos x-1)\\ \sqrt{3} \cos x \sin 2x (2 \cos x -1)=2\cos x \sin^2x(2\cos x-1)\\ \cos x (2 \cos x -1)( \sqrt{3} \sin 2x -2\sin^2x)=0\\ \cos x (2 \cos x -1)( 2\sqrt{3} \sin x \cos x -2\sin^2x)=0\\ 2 \sin x \cos x (2 \cos x -1)( \sqrt{3} \cos x -\sin x)=0\\ \sin2x (2 \cos x -1)( \sqrt{3} ctg x -1)=0$
$\sin2x=0$ или $\cos x=\frac{1}{2}$ или $ctg x=\frac{\sqrt{3}}{3}$
Решаем каждое из полученных уравнений:
$1)\ \sin2x=0\ \Rightarrow 2x=\pi k \ \Rightarrow x=\frac{\pi k}{2}$
C учетом О.Д.З. $x=\frac{\pi}{2} +\pi n,\ n \in Z$
$2)\ \cos x =\frac{1}{2}$ противоречит О.Д.З. ⇒ решений нет.
$3)\ ctg x = \frac{\sqrt{3}}{3} \Rightarrow x=\frac{\pi}{3}+\pi n$
а с учетом О.Д.З. $x=-\frac{2\pi}{3}+ 2\pi n,\ n \in Z$
Ответ: $\frac{\pi}{2}+\pi n;\ -\frac{2\pi}{3}+2\pi n,\ n \in Z$
- Автор:
  narcisoyswk
- 6 лет назад
- 0
task/29376552
----------------------
√3cosx(sin3x +sinx -sin2x) / (2cosx - 1) = 2cosx / (ctg²x +1) ;
ОДЗ : { 2cosx - 1 ≠ 0 , sinx ≠ 0 . * * * ctgx = cosx /sinx * * *
√3cosx(2sin2xcosx - sin2x) / (2cosx - 1) = 2cosx / (ctg²x +1) ;
√3cosx*sin2x(2cosx - 1) / (2cosx - 1) = 2cosx / (ctg²x +1) ;
√3cosx*sin2x =2cosx*sin²x⇔√3cosx*2sinx*cosx = 2cosx*sin²x || :2sin²x ≠ 0 || ⇔ √3cosx*ctgx = cosx ⇔
√3cosx(ctgx - 1/√3) = 0 ;
а)
cosx = 0 ⇒ x = π/2 + πn , n ∈ ℤ ;
или
б)
ctgx - 1/√3 = 0 ⇔ ctgx = 1/√3 ⇒ x = π/3 + πn , n ∈ ℤ .
c учетом cosx ≠ 1/2 : x =4π/3 + 2πn , n ∈ ℤ .
ответ : π/2 +πn ; 4π/3 + 2πn , n ∈ ℤ .
==================
P.S. sin3x+sinx = 2sin2x*cosx ; sinα + sinβ = 2sin(α+β)/2*cos(α - β)/2 .
- Автор:
  buttercup
- 6 лет назад
- 0
Добавить свой ответ