Задать вопрос Регистрация
Помочь другим

  • Помогите решить это, знаю что ответ должен получиться 1,25

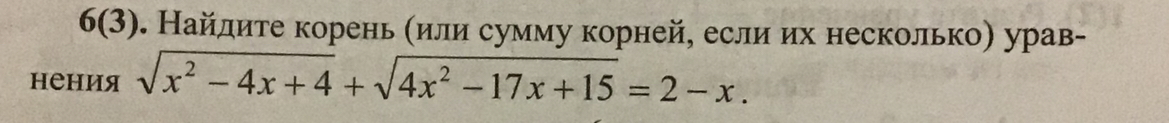
    question img

Ответы 1

  • ОДЗ:

    \left\{\begin{array}{I}\bf 2-x \geq 0 \\ \bf 4x^2-17x+15 \geq 0 \end{array}} \Leftrightarrow \ \left\{\begin{array}{I} \bf x \leq 2 \\ \bf (4x-5)(x-3) \geq 0 \end{array}} \ \Leftrightarrow \ \left\{\begin{array}{I}\bf x \leq 2 \\ \bf x \in (- \infty; \ \dfrac{5}{4}] \cup [3; \ +\infty) \end{array}}

    x∈(-∞; 5/4]

    \bf\sqrt{x^2-4x+4} + \sqrt{4x^2-17x+15}=2-x \\ \sqrt{(x-2)^2}+ \sqrt{4x^2-17x+15}=2-x \\ \sqrt{4x^2-17x+15}=2-x-|x-2|

    x≤5/4 по ОДЗ. Модуль раскрываем с минусом.

    \bf \sqrt{4x^2-17x+15}=2-x+x-2 \\ 4x^2-17x+15=0 \\ x_1=\dfrac{5}{4} \ \ \ \ \ x_2=3 otin ODZ

    Ответ: 5/4

    • Автор:

      queen75
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years